Matrice élémentaire - Définition
Une matrice est dite élémentaire lorsqu'elle est obtenue par des opérations élémentaires sur les lignes ou colonnes de la matrice identité.
Les opérations élémentaires sur une matrice sont les suivantes :
- échanger deux lignes ou deux colonnes
- ajouter un multiple d'une ligne à une autre ligne (respectivement colonne)
- multiplier une ligne ou une colonne par un scalaire différent de zéro
Exemples
| Opération effectuée sur la matrice identité I3 | type de matrice | |
| permutation ligne 1 et 2 |
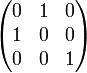
|
matrice de permutation |
| ligne n°3 * 5 |
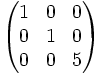
|
matrice de dilatation |
| ligne n°3 + 5*ligne n°2 |
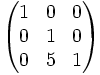
|
matrice de transvection |
Multiplier à gauche une matrice A par une matrice élémentaire revient à effectuer l'opération élémentaire correspondante sur les lignes de A. Multiplier A à droite par une matrice élémentaire revient à faire une opération sur les colonnes.

















































