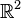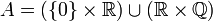Espace localement connexe - Définition

Définition d'un espace localement connexe

Soit un espace topologique. On dit que est localement connexe si tout voisinage de tout point de contient un voisinage connexe de (pour la topologie induite par la topologie de ).

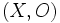
Cela signifie que tout point de cet espace topologique admet une base de voisinages connexes.

La connexité locale n'est pas préservée par image continue.

Un espace topologique est localement connexe si et seulement si, pour tout ouvert , les composantes connexes de sont ouvertes.

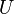
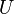
Exemples

Les exemples les plus classiques d'espace topologique localement connexes sont , , ...

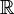
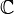
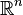
Un exemple d'espace connexe qui n'est pas localement connexe: dans muni de la topologie usuelle on considère la partie . Alors A est connexe mais n'est pas localement connexe. En particulier, tout point de A possède dans A un voisinage connexe (à savoir A lui-même) mais ne possède pas forcément de base de voisinages connexes.