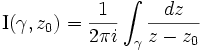Lacet (mathématiques) - Définition
En mathématiques, un lacet est la modélisation d'une " boucle ". C'est une courbe continue et fermée, c'est-à-dire que ses extrémités sont confondues. La notion de lacet est utile en analyse complexe et en topologie.
Définitions
Si


![\gamma \, : \, [0,1] \rightarrow X \,\!](https://static.techno-science.net/illustration/Definitions/autres/f/ff47807126bd5ccc396f204424ea985f_435c8b1bd013a2dee4559074b2824f95.png)
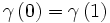
Autre définitions :
- Un lacet sur


- Un lacet sur

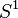

-
- (où
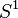
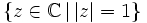
- (où
En analyse complexe on s'intéresse aux lacets qui sont aussi des courbes rectifiables.
On peut aussi définir les lacets polygonaux, ou de classe
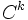
Indice dans le plan complexe
Dans le cas
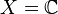
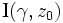
![z_0\in\mathbb{C} \setminus \gamma([0, 1])](https://static.techno-science.net/illustration/Definitions/autres/b/b9bd5158d1efc6db62072df9c53997f6_317a1798b47d5530cf81396788e4bc0d.png)
On peut l'obtenir en calculant :