Propriété locale - Définition

On dit d'une certaine propriété mathématique qu'elle est localement vérifiée en un point d'un espace topologique s'il existe un voisinage de ce point sur lequel la propriété est vraie.

On dit d'une certaine propriété mathématique qu'elle est localement vérifiée si elle est localement vérifiée en tout point de l'espace topologique considéré.

Cette notion se retrouve dans tous les domaines des mathématiques qui utilisent la topologie, en particulier en analyse.

Par exemple :

• On dit qu'une fonction définie sur un espace topologique admet en en point de un maximum local s'il existe un voisinage de tel que soit la plus grande valeur de sur .
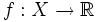
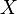
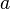
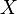
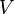
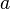
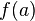
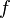
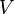
• On dit qu'un espace topologique est localement compact s'il est séparé et si chacun de ses points possède un voisinage compact.