Point isolé - Définition
En topologie, un point x d'un espace topologique E est dit isolé si le singleton
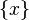
Autres formulations équivalentes :
-
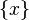
- x n'est pas adhérent à
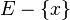
Exemple : dans l'espace topologique
![\{ 0 \} \cup [1,2] \,\!](https://static.techno-science.net/illustration/Definitions/autres/4/4189a655bcd14040f6a466b71853337d_2de21458d42783b378258c498afcc360.png)
Un espace topologique dans lequel tout point est isolé est dit discret.

















































