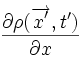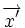Description eulérienne - Définition

Pour décrire mathématiquement les propriétés d'un fluide en mouvement, deux systèmes cohabitent, l'un et l'autre présentant des avantages dans des situations particulières. Il s'agit de la description lagrangienne et de la description eulérienne.

La description eulérienne consiste à se placer en un point fixe du milieu à l'étude et à observer les modifications des propriétés du fluide qui défile en ce point.

Dans le cadre de cette description, les propriétés locales du fluide sont fonction de et de t, et une même propriété, mesurée en un même point à deux temps différents correspond à deux particules fluides distinctes.

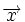
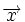
C'est la description que l'on utilise le plus souvent dans les problèmes de dynamique des fluides, car elle permet de calculer facilement la variation spatiale d'une propriété du fluide au temps t. La dérivée partielle de la densité est alors la mesure du taux de modification de la densité autour du point , au temps t' fixé, comme on pourrait l'obtenir en prenant une photo de la densité de l'écoulement puis en dérivant par rapport à la variable spatiale.