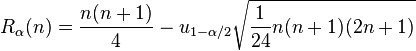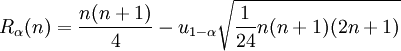Test (statistique) - Définition
Principe d'un test statistique
Le but d'un test statistique est de tester une hypothèse concernant un ensemble de données.
Exemple
On dispose de N réalisations d'une loi que l'on sait normale (espérance μ et variance 1), on désire tester l'hypothèse :
- H0 : μ = 0
contre :
- H1 :
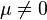
Calculons
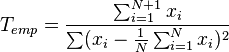
Sous l'hypothèse H0, nous connaissons la distribution de cette statistique. Nous pouvons alors évaluer sa vraissemblance en calculant une p-value :
![p_{value} = P^{H_0}[T \ge T_{emp}]](https://static.techno-science.net/illustration/Definitions/autres/3/3527f828778b00ddea345d4d617a79bc_fcc6e3a8e0f86480d221eff2566389fb.png)
Différents types d'erreurs
Dans la pratique, les tests statistiques conduisent à deux types d'erreurs :
- Rejet à tort de l'hypothèse H0 : erreur de première espèce.
- Acceptation à tort de l'hypothèse H0 : erreur de seconde espèce.
Il est alors possible de contrôler α, le taux d'erreur de première espèce :
- Si pvalue < α : On rejette H0
- Si pvalue > α : On accepte H0
Remarque : Dans les livres Statistiques il est marque que Rejet de Ho ssi pvalue < α [1]
D'après Gujarati [2] la pvalue est le niveau significatif le plus bas où l'hypothèse nulle peut-être rejetée (traduction faite par mes soins, il se peut qu'elle ne soit pas exacte à 100 %) ainsi donc si pvalue > α alors on ne rejette pas
Schématiquement : Soit α = 5%
Si P-Value = 0,03 :
0%---1%---2%---3%---4%---5%---6%---7%---8%---9%---10%
]...Non Rejet..[...............Rejet...............[
Hors à 5%, on rejette --> RHo
Si P-Value = 0,05 :
0%---1%---2%---3%---4%---5%---6%---7%---8%---9%---10%
].......Non Rejet........[..........Rejet..........[
Hors à 5%, on a le niveau le plus bas qu'on rejette, ce niveau est compris dans le test --> RHO
Si P-Value = 0,07 :
0%---1%---2%---3%---4%---5%---6%---7%---8%---9%---10%
]............Non Rejet.............[.....Rejet.....[
Hors à 5%, on ne rejette pas --> Non rejet de Ho (ce qui est différent d'acceptation de Ho qui dépendra du test de seconde espèce)
Liste des tests statistiques
Test du T
- H0 : μ = μ0
- H1 : μ > μ0
Test du U
- H0 : μ = μ0
- H1 : μ > μ0
Test du U
- H0 : π = p0
- H1 : π > p0
Test du χ2
- H0 : σ>2 = σ02
- H1 : σ>2 > σ02
Test du U
Test du U
Test du F
Test du χ2
Test du T
Test de Fisher-Student
Test de Spearman
Tests non paramétriques
Test de Mann-Whitney
Le test de (Wilcoxon-) Mann-Whitney est un test non paramétrique d'identité portant sur deux échantillons indépendants issus de variables numériques ou ordinales.
Ces deux jeux peuvent contenir des nombres différents d'observations, ou même faire référence à deux variables différentes.
1) C'est un test d'identité : il porte sur le fait que deux séries de valeurs numériques (ou ordinales) sont issues d'une même distribution.
2) Il est non paramétrique, c'est à dire qu'il ne fait aucune hypothèse sur les formes analytiques des distributions F1(x) et F2(x) des populations 1 et 2. Il teste donc l'hypothèse :
H0 : "F1 = F2"
3) Il utilise non pas les valeurs prises par les observations, mais leur rangs une fois ces observations réunies dans un même ensemble.
de tester une hypothèse concernant un ensemble de données.
Exemple [modifier]
On dispose de N réalisations d'une loi que l'on sait normale (espérance μ et variance 1), on désire tester l'hypothèse :
Le test de Mann-Whitney a donc le même objectif qu'un autre test d'identité important, le "Test du Chi-2 d'identité", dans sa version pour variable numérique. Si les populations sont supposées normales et de même variance, le test t aura la préférence.
Le test de Kruskal-Wallis peut être perçu comme une extension du test de Mann-Whitney à plus de deux échantillons (de même que ANOVA univariée est une extension du test t à plus de deux échantillons).
Test du signe
Test de Wilcoxon