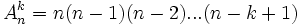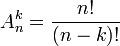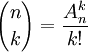Arrangement (mathématiques) - Définition
La notion d'arrangement est utilisée en probabilités, et notamment pour les dénombrements en analyse combinatoire.
Considérons un ensemble formé de n éléments. On prend k éléments (k < n) et on en constitue une liste ordonnée sans répétition possible, c'est-à-dire dans laquelle l'ordre des éléments est pris en compte (si l'on permute deux éléments de la liste, on a une liste différente, et un élément ne peut être présent qu'une seule fois). Une telle liste ordonnée est appelée un arrangement. Le nombre d'arrangements que l'on peut faire est noté
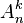
Cette formule peut se comprendre à l'aide d'un arbre des choix successifs, puisque le premier élément est choisi parmi n, le second parmi (n-1) ... et le dernier parmi (n-k+1). Avec la notation factorielle, où n! = 1×2×...n, cette formule devient
Akn est en fait le nombre d'injections que l'on peut faire d'un ensemble à k éléments vers un ensemble à n éléments. Le nombre d'arrangements est lié au coefficient binomial
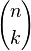
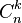
Exemples d'arrangements :
- une phrase sans répétition de mot est un arrangement du dictionnaire ;
- une association forme son bureau (président, trésorier, secrétaire) à partir des membres de l'association ; le bureau est un arrangement de l'association ;
- le podium d'une course est un arrangement de l'ensemble des participants.