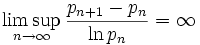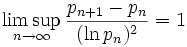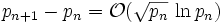Conjecture de Cramér - Définition

En mathématiques, la conjecture de Cramér, formulée par le mathématicien suédois Harald Cramér en 1936, énonce que

où p_n est le n-ième nombre premier ; cette conjecture n'est pas démontrée à ce jour. Cramér a aussi formulé une autre conjecture concernant les nombres premiers, énonçant que

qu'il a démontrée sous l'hypothèse de Riemann (qui elle-même n'est pas encore démontrée non plus).

quant à elle est démontrée comme vraie.