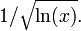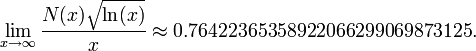Constante de Landau-Ramanujan - Définition
En mathématiques, la constante de Landau-Ramanujan apparaît dans un résultat de théorie des nombres qui énonce que la proportion des entiers positifs inférieurs à x qui sont la somme de deux carrés est, pour un grand x, grossièrement proportionnelle à
La constante de proportionnalité est la constante de Landau-Ramanujan.
Plus formellement, si N(x) est le nombre d'entiers positifs inférieurs à x qui sont la somme de deux carrés, alors