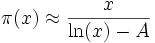Constante de Legendre - Définition
La constante de Legendre est une constante mathématique proposée par le mathématicien Adrien-Marie Legendre et qui n'a aujourd'hui plus qu'un intérêt historique.
Avant la découverte du théorème des nombres premiers, on cherchait à évaluer la fonction π(x), le nombre de nombres premiers inférieurs à x.
L'examen des données numériques accumulées pour les nombres premiers connus à l'époque avait conduit Legendre à conjecturer que, pour les grandes valeurs de x :
où A, selon Legendre, devait valoir environ 1,08366.
Ce nombre A a été appelé constante de Legendre.
Plus tard, le mathématicien allemand Gauss examina aussi les données numériques et conclut que la constante A devait être inférieure à la valeur proposée par Legendre. En fait, il semblerait que cette constante soit égale à 1.