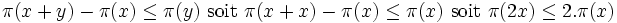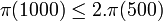Seconde conjecture de Hardy-Littlewood - Définition
En théorie des nombres, la seconde conjecture de Hardy-Littlewood concerne le nombre de nombres premiers.
Soit π(x) le nombre de nombres premiers p tels que p ≤ x, la conjecture postule que
- π(x + y) - π(x) ≤ π(y)
pour tous x, y ≥ 2.
Ce qui signifie que le nombre de nombres premiers entre x + 1 et x + y est toujours inférieur ou égal au nombre de nombres premiers entre 1 et y. Ceci est probablement faux en général et incompatible avec la première conjecture de Hardy-Littlewood ainsi que l'a démontré Richards de manière non évidente en 1974. Il est vraisemblable que la conjecture sera infirmée pour de très grandes valeurs de x et y.
il n'y aurait pas un problème avec cette formulation. Si on pose x = y, cela donne :
Par exemple :