Arithmétique (mathématiques élémentaires) - Définition

L'arithmétique est la partie des mathématiques consacrée à l'étude des nombres. La totalité des nombres ont été regroupés par groupes, appelés " ensembles " par les mathématiciens. ces ensembles sont:

•  : l'ensemble des entiers naturels ( etc.)
•  : l'ensemble des entiers relatifs ( etc.)
•  : l'ensemble des nombres décimaux, c'est-à-dire qui s'écrivent avec un nombre fini de décimales .
•  : l'ensemble des nombres rationnels, c'est-à-dire des nombres pouvant s'écrire comme la fraction de deux décimaux .
•  : l'ensemble des nombres réels, c'est-à-dire ceux dont la partie imaginaire est nulle (π, le nombre d'or, )
•  : nombres complexes regroupe tous les nombres usuels.

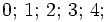
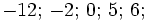
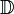
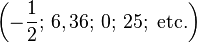
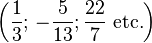
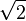
On remarquera que chaque ensemble est inclus dans l'ensemble qui lui est " supérieur ". Ainsi, tous les éléments de appartiennent aussi à , par exemple. Mais à l'inverse, un élément de n'est pas forcément élément de . On peut représenter ces ensembles par des cercles concentriques: le plus petit est , puis viennent , , , et .

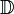
Il est possible de ne considérer qu'une partie d'un ensemble. Ainsi, on notera l'ensemble des nombres positifs de . De même on notera l'ensemble privé de 0. On remarque entre autre que et que (il s'agit de " privé de " .)

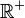
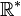
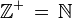
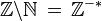
Certains nombres possèdent des propriétés remarquables. C'est le cas des nombres dits premiers. Ce sont des éléments de possédant uniquement deux diviseurs positifs distincts, à savoir 1 et eux-même. Les premiers nombres premiers sont 2; 3; 5; 7; 11; 13; 17 etc. 1 n'est pas premier car il n'a pas 2 diviseurs distincts, mais un seul. Il existe une infinité de nombres premiers. En complétant une grille de taille 10 10 avec les 100 premiers entiers non nuls, et en rayant ceux qui ne sont pas premiers, on obtient les nombres premiers appartenant à par un procédé appelé un crible d'Eratosthène, du nom du savant grec qui l'inventa.

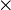
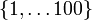
Les entiers naturels sont divisés en deux catégories bien connues des joueurs de roulette: les pairs et les impairs.
Un entier n pair est un multiple de 2 et peut être noté , avec Un nombre n impair n'est pas multiple de 2 et se note , avec .

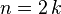
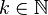
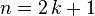
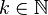
On montre que tout entier est soit pair soit impair, et au moins l'un des deux, et ce pour un unique k : on note
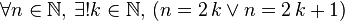
Les premiers entiers pairs sont 0, 2, 4, 6, 8, 10 ... Les premiers entiers impairs sont 1, 3, 5, 7, 9, 11 ...

Les nombres et leurs combinaisons possèdent de nombreuses propriétés.