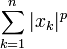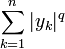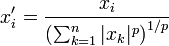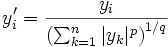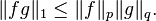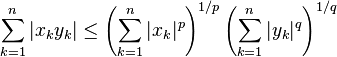Inégalité de Hölder - Définition
En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans Lq(S). Alors fg appartient à L1(S) et
En considérant S comme l’ensemble {1,...,n} avec la mesure de dénombrement, nous obtenons un cas particulier de l’inégalité :
valable pour tous réels (ou nombres complexes) x1,...,xn, y1,...,yn.
En considérant S comme l’ensemble des entiers naturels avec la mesure de dénombrement, nous obtenons une inégalité similaire pour les séries.
Pour p = q = 2, nous obtenons l’inégalité de Cauchy-Schwarz.
L’inégalité de Hölder est utilisée pour démontrer l' inégalité triangulaire dans l’espace Lp, parfois appelée inégalité de Minkowski et aussi pour établir que Lp est le dual de Lq si
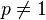
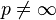
La concavité de la fonction logarithme népérien permet d'écrire, pour tout réels strictements positifs a et b, vu que
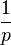

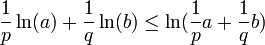
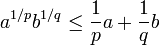
Supposons dans un premier temps
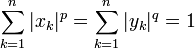
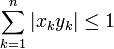
Supposons désormais simplement que