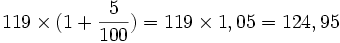Pourcentage - Définition
Un pourcentage est une façon d'exprimer une proportion ou une fraction dans un ensemble. Une expression comme " 45 % " (lue " 45 pour cent ") est en réalité la sténographie pour la fraction 45/100 dont l'écriture décimale est 0,45. Dans certaines situations, on préfère le terme de taux.
Histoire du symbole
La notation "%" dès le XVIIIe siècle, notez la barre diagonale.
|
À l'origine, les traités mathématiques en latin n'étaient pas notés à l'aide de chiffres et de symboles, mais uniquement en mots. Ainsi, l'expression de la fraction 1/100 s'écrivait unu per cento.
Plus tard, vers 1425, cette écriture fut simplifiée, en plaçant un P couché sur le cento.
Dès 1650, les traités abrégèrent également cento, ne gardant que le o final, ce qui donnait une forme presque similaire au % actuel, avec une barre horizontale au lieu de diagonale.
Dès le début XVIIIe siècle, le % gardera sa forme actuelle
Calculs élémentaires
Exemple 1
- Dans une assemblée de 50 personnes, il y a 31 femmes. Celles-ci représentent 62 % du total car
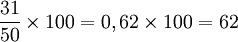
Exemple 2
- Un commerçant fait une remise de 6 € sur le prix d'un article coûtant 119 €. Le pourcentage de remise par rapport au prix est d'environ 5 % car
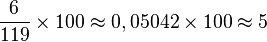
Exemple 3
- Le prix hors taxes d'un objet est 119 €. Le taux de TVA est de 5 %. Celle-ci s'élève donc à
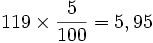
Variation en pourcentage
Dans l'exemple de la TVA ci-dessus, le prix TTC peut s'obtenir en une seule opération grâce au coefficient multiplicateur :
Plus généralement, une augmentation de t % se traduit par une multiplication par
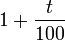
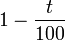
Des variations successives à taux fixe conduisent à des progressions géométriques. Ainsi, augmenter 35 fois de 2 % revient à multiplier par 1,0235, c'est-à-dire quasiment par 2. Et diminuer 35 fois de 2 % revient à multiplier par 0,9835, c'est-à-dire à diviser par un peu plus de 2.
Erreurs courantes
Une utilisation irréfléchie des pourcentages peut aboutir à des conclusions fausses. Cette liste n'est pas exhaustive.
- Exemple 1 :
- Un journaliste a titré bravement " Le prix des CD a diminué de 700 % en 5 ans. " S'il voulait dire que leur prix avait été divisé par 7, il devait annoncer une diminution de 85,7 %. On entend aussi des fois parler d'augmentations " de 120 % " alors que ce n'est qu'une augmentation de 20 % ; augmenter de 120 % revient à multiplier par 1 + 1,2 = 2,2. Pour augmenter de 20 % il s'agit de multiplier par 1 + 20/100 = 1,2.
- Exemple 2 :
- Si un objet est vendu 100 € TTC avec un taux de TVA de 18,6 %, le montant de la TVA n'est pas de 18,60 € mais de 15,68 €. En effet, la formule est
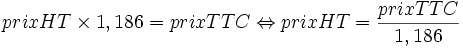
- Exemple 3 :
- Une augmentation de N pour cent suivie d'une diminution au même taux ne revient pas à laisser la valeur identique (de même dans le sens inverse, pour une diminution suivie d'une augmentation). Cela car l'augmentation de N pour cent revient à la multiplication par
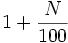
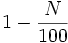
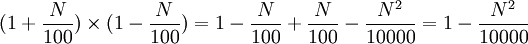
- Par exemple, suite à une baisse d'un prix de 20 %, il faudrait ensuite l'augmenter de 25 %, puisque
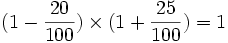
Typographie
Le signe " % " en typographie française doit être précédé et suivi d'une espace forte[1]. Dans d'autres langues, et notamment en anglais, le signe est collé au chiffre.