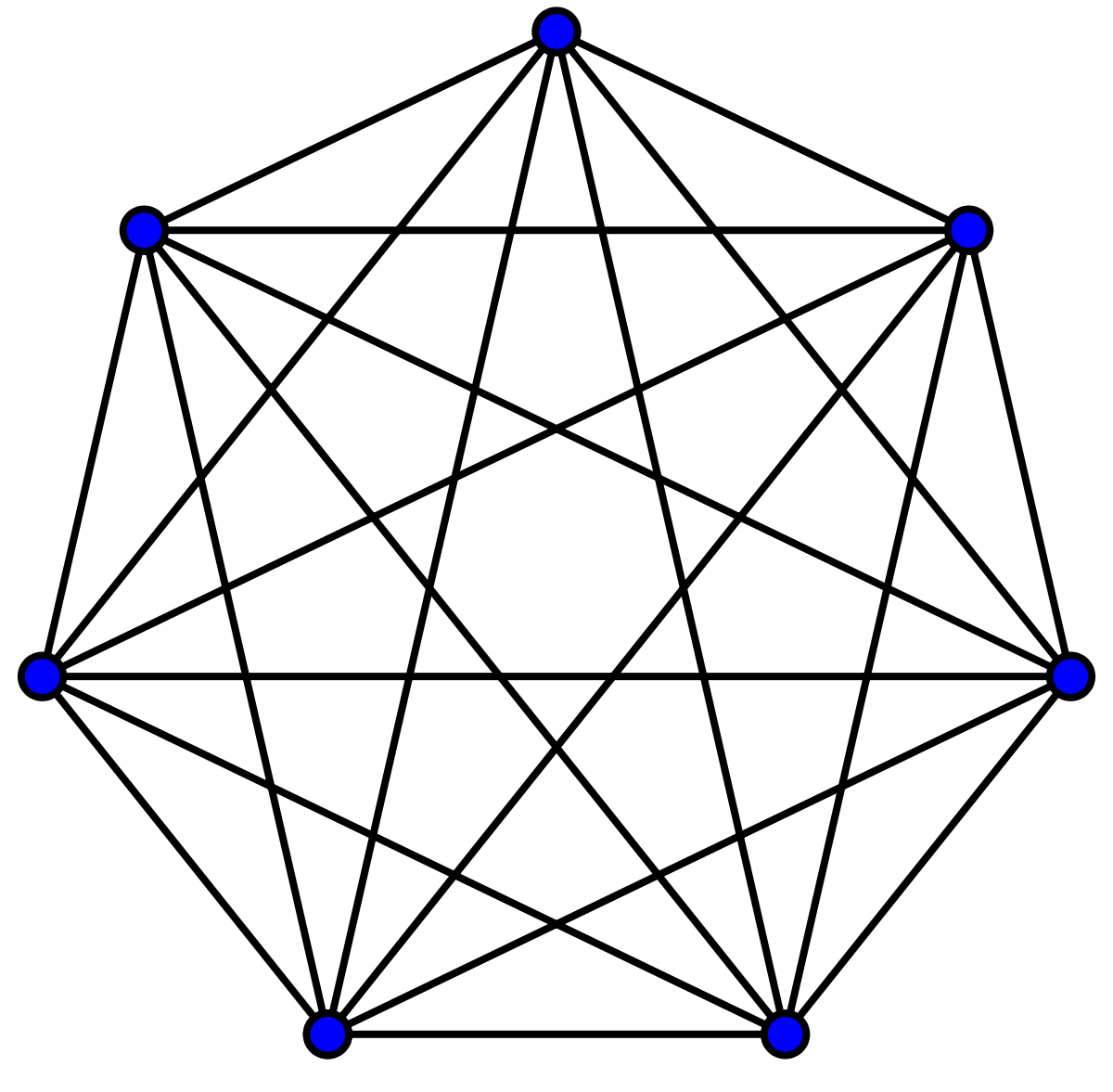
Graphe complet - Définition

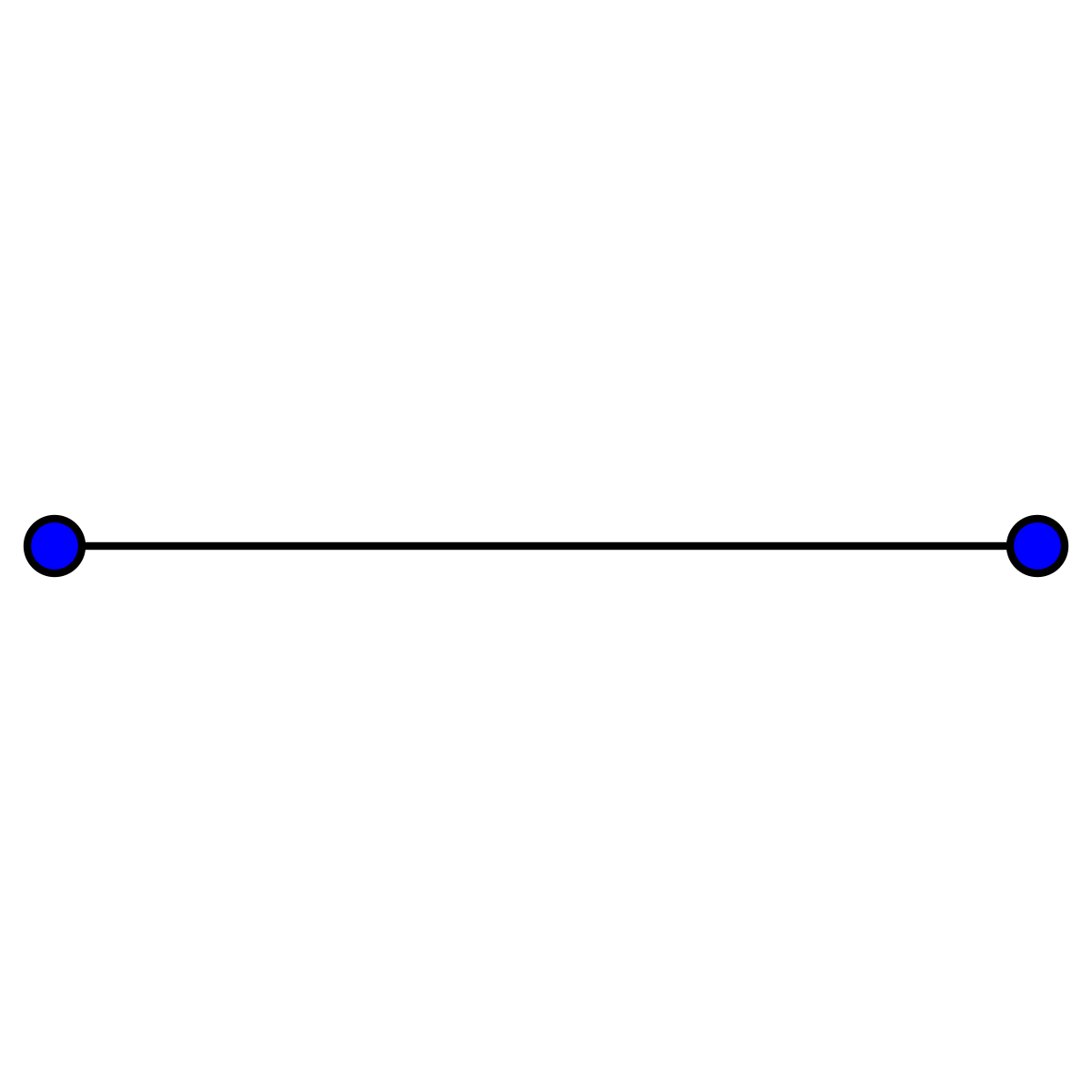
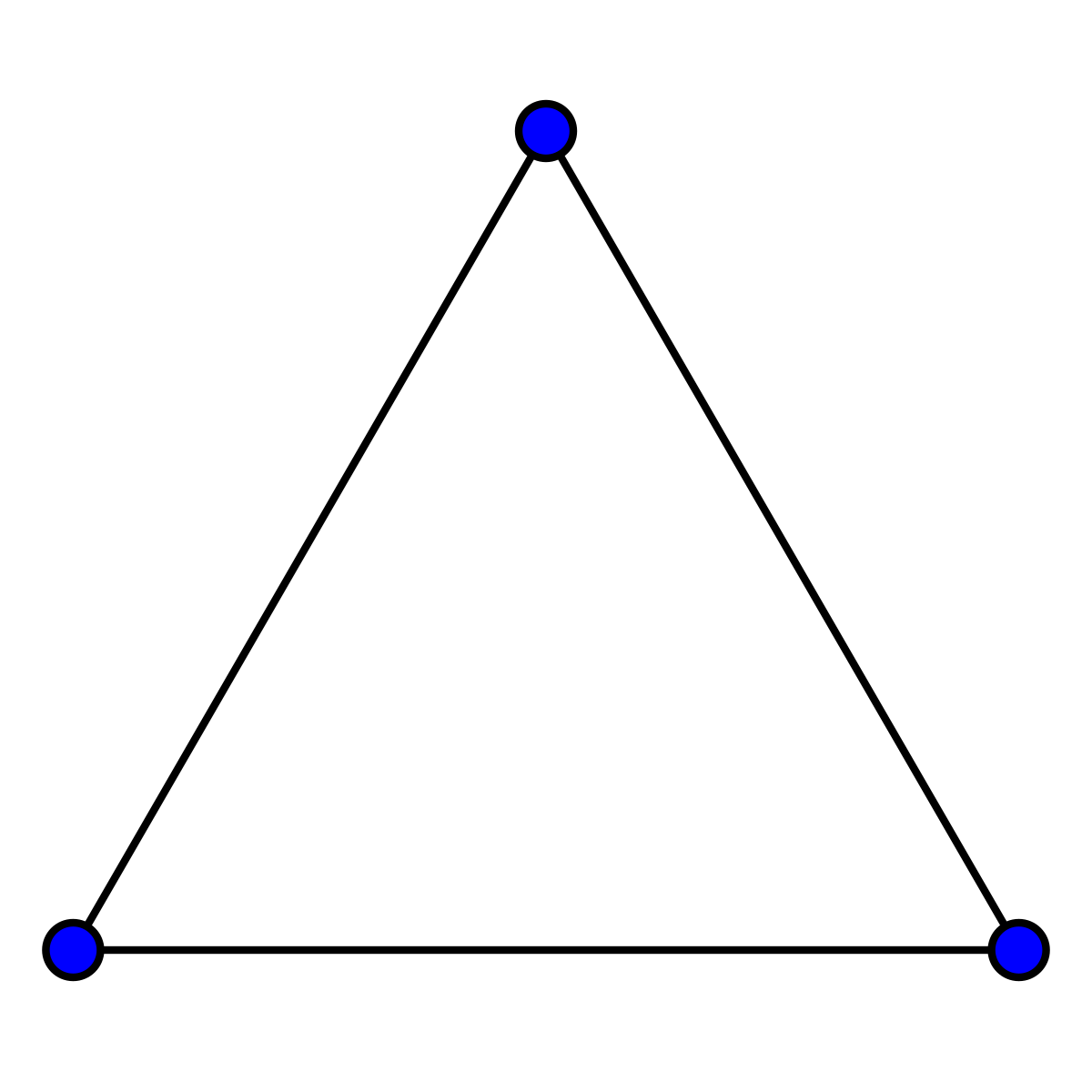
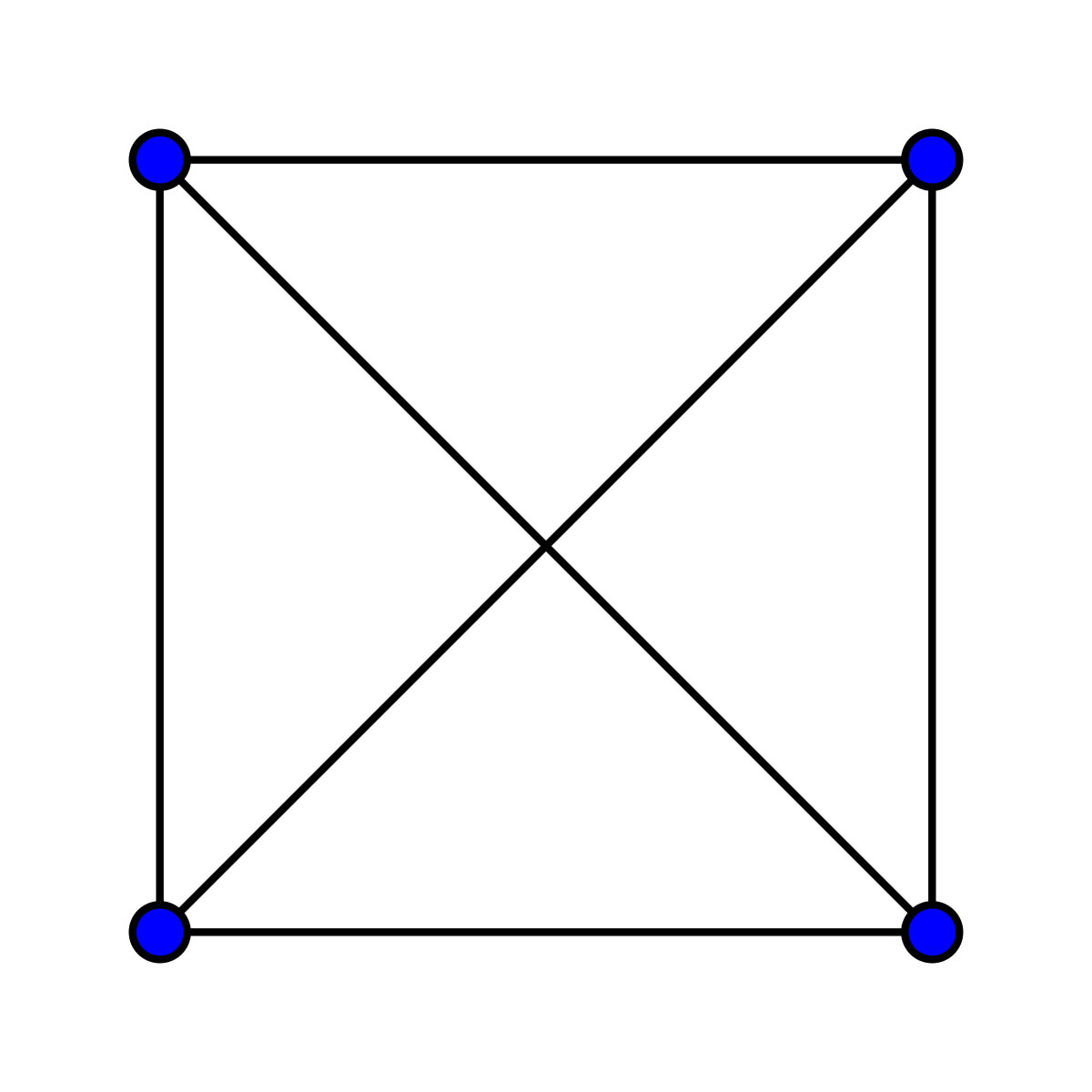
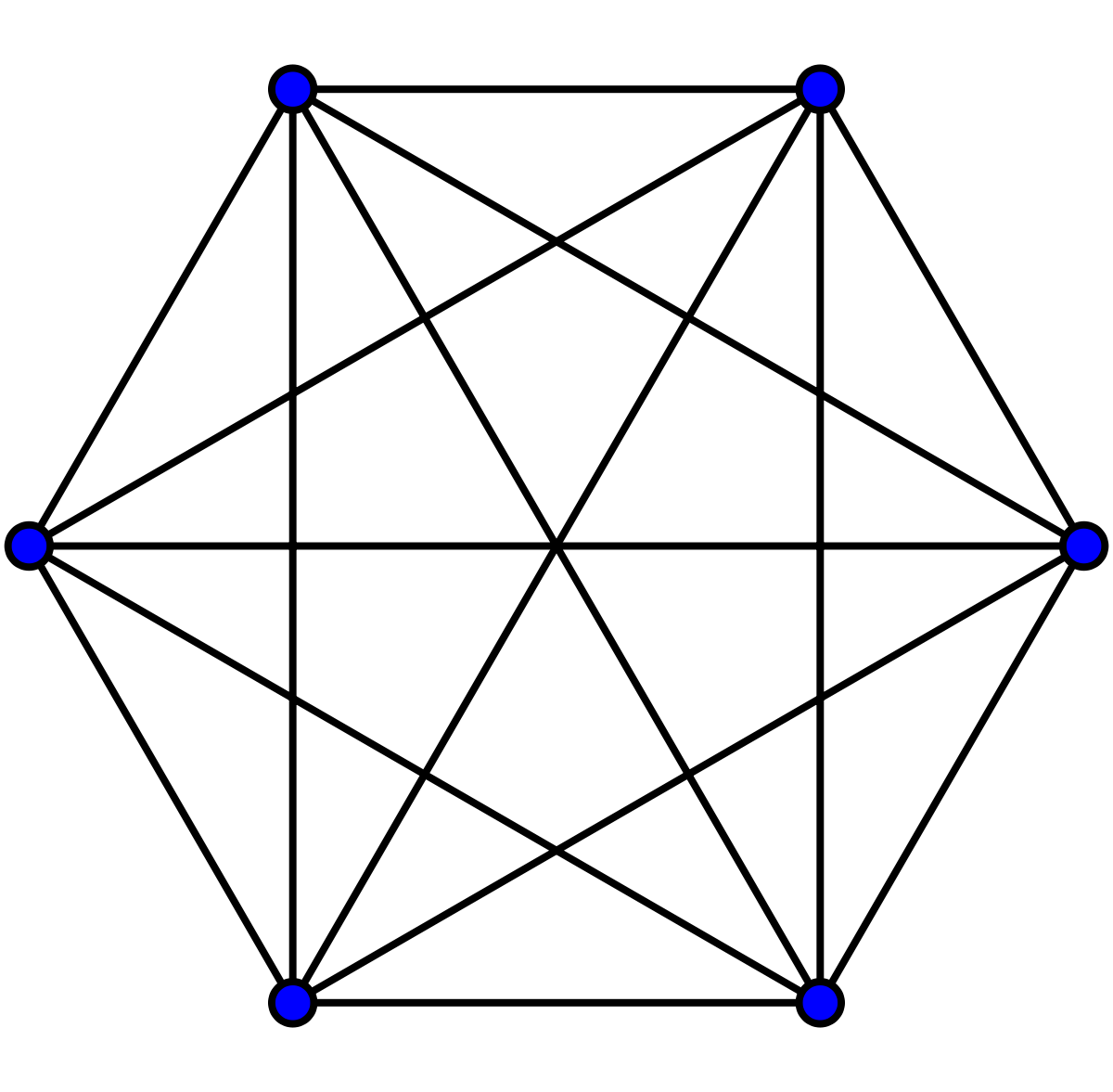
Un graphe complet est un graphe dont les sommets sont tous reliés deux à deux par une arête. Dans un graphe G, on nomme clique un sous-graphe complet de G, c'est-à-dire une partie de l'ensemble des sommets de G telle que le graphe induit par G sur cette partie soit un graphe complet. Un des problèmes centraux de la théorie des graphes consiste à chercher la clique de taille maximum dans un graphe.

Un graphe complet à n sommets contient arêtes. On note K_n le graphe complet d'ordre n, c'est-à-dire contenant n sommets.

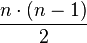
Le graphe K₅ est un exemple minimal de graphe non-planaire.

K1	K2	K3	K4
K5	K6	K7	K8