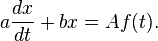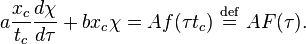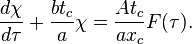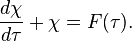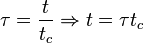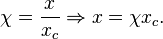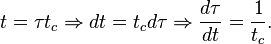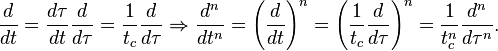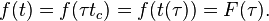Adimensionnement - Définition

Étapes de l'adimensionnement

L'adimensionnement d'un système d'équations s'effectue selon la démarche suivante :

1. Identifier toutes les variables indépendantes et dépendantes ;
2. Remplacer chacune d'elles par une quantité normalisée par rapport à l'unité de mesure caractéristique à déterminer ;
3. Diviser par le coefficient du terme de plus grand ordre ;
4. Choisir judicieusement la définition de l'unité caractéristique pour chaque variable de façon à obtenir des coefficients égaux à 1 pour le plus grand nombre de termes possible ;
5. Réécrire le système d'équations en fonction de leurs nouvelles quantités sans dimension.

Les trois dernières étapes sont habituellement spécifiques au problème auquel on applique l'adimensionnement. En revanche, les deux premières étapes sont indispensables pour pratiquement tous les systèmes.

À tite d'exemple, considérons une équation différentielle du premier ordre à coefficients constants :

1. Dans cette équation, la variable indépendante est t et la variable dépendante x.
2. Posons . Il en découle l'équation

   

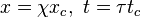
3. Le coefficient du terme de plus grand ordre est celui de la première dérivée. La division donne

   

4. Le coefficient de χ contenant uniquement une variable caractéristique t_c, il est plus facile de commencer par ce terme :

   Il en résulte

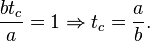
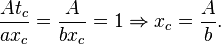
5. L'équation finale adimensionnée devient dans ce cas complètement indépendante des paramètres avec unités :

   

Substitutions

Considérons un système simple caractérisé par deux variables : une variable dépendante x et une variable indépendante t, où x est une fonction de t. x et t représentent tous deux des quantités avec unité. Pour normaliser ces deux variables, supposons qu'il existe deux unités de mesure intrinsèques x_c et t_c dont les unités sont respectivement les mêmes que x et t, telles que les conditions suivantes soient remplies :

Ces équations sont utilisées pour remplacer x et t lors de l'adimensionnement. Si des opérateurs différentiels sont nécessaires pour décrire le système original, leurs homologues normalisés deviennent des opérateurs différentiels sans dimension.

Conventions

Bien que les noms destinés à remplacer x et t ne fassent l'objet d'aucune restriction, on les choisit généralement de telle sorte qu'ils paraissent commodes et intuitifs lors de leur utilisation dans le problème considéré. Par exemple, si x représente la masse, la lettre m pourrait être un symbole approprié pour représenter la quantité de masse sans dimension.

Dans cet article, les conventions suivantes sont utilisées :

• t représente la variable indépendante, habituellement une quantité de temps. Son homologue adimensionné est τ.
• x représente la variable dépendante, qui peut être une masse, une tension électrique ou toute autre quantité mesurable. Son homologue adimensionné est χ.

Un c souscrit ajouté au nom d'une variable associée à une quantité est utilisé pour indiquer l'unité caractéristique utilisée pour normaliser cette quantité. Par exemple, si x est une quantité, alors x_c est l'unité caractéristique utilisée pour la normaliser.

Opérateurs différentiels

Considérons la relation

L'expression des opérateurs différentiels sans dimension par rapport à la variable indépendante devient

Fonction de forçage

Si un système possède une fonction de forçage f(t), alors

Ainsi, la nouvelle fonction de forçage F est rendue dépendante de la quantité sans dimension τ.