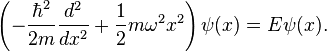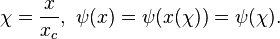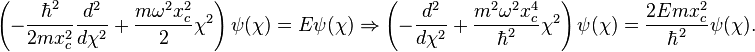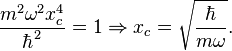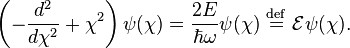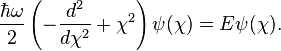Adimensionnement - Définition
La liste des auteurs de cet article est disponible ici.
Exemple d'équation différentielle non linéaire
Comme il n'existe pas de méthode générale de résolution des équations différentielles non linéaires, chaque cas doit être traité individuellement lors de l'adimensionnement.
Oscillateur harmonique quantique
L'équation de Schrödinger pour un oscillateur harmonique quantique à une dimension indépendant du temps est la suivante :
La fonction d'onde ψ elle-même représente une probabilité, qui est d'une certaine façon déjà sans dimension et normalisée. Il n'est donc pas nécessaire d'adimensionner la fonction d'onde. Cependant, elle doit être réécrite comme une fonction d'une variable sans dimension. En outre, la variable x a une unité de type longueur. Substituons alors
L'équation différentielle devient
Pour rendre le terme devant χ² sans dimension, posons
L'équation adimensionnée complète ainsi obtenue est
Le facteur d'adimensionnement pour l'énergie est le même que celui de l'état fondamental de l'oscillateur harmonique. Habituellement, le terme correspondant à l'énergie n'est pas rendu sans dimension car l'un des objets principaux de la mécanique quantique est de déterminer les énergies des états d'un système. En réarrangeant la première équation, on retrouve l'équation familière de l'oscillateur harmonique