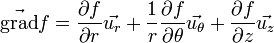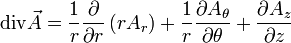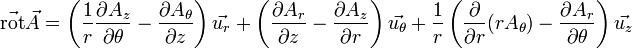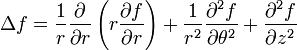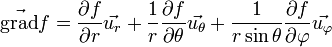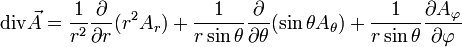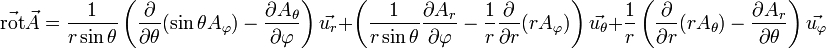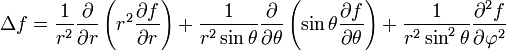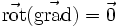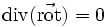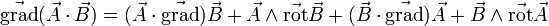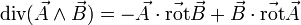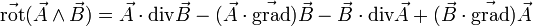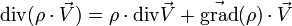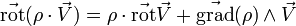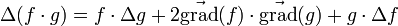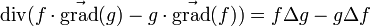Mercredi 30 Avril 2025
Rechercher 🔍

Analyse vectorielle - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Principaux opérateurs différentiels linéaires de tri - Opérateurs d'ordre supérieur - Application linéaire tangente d'un champ de vecteurs - Expressions des opérateurs en différentes coordonnées - Quelques formules différentielles

Expressions des opérateurs en différentes coordonnées

Coordonnées cylindriques

\vec{\mathrm{grad}}f=\frac{\partial f}{\partial r}\vec{u_r}+\frac{1}{r}\frac{\partial f}{\partial \theta}\vec{u_\theta}+\frac{\partial f}{\partial z}\vec{u_z}
\mathrm{div}\vec{A}=\frac{1}{r}\frac{\partial}{\partial r}\left(rA_r \right)+\frac{1}{r}\frac{\partial A_\theta}{\partial \theta}+\frac{\partial A_z}{\partial z}
\vec{\mathrm{rot}}\vec{A}=\left(\frac{1}{r}\frac{\partial A_z}{\partial \theta}-\frac{\partial A_\theta}{\partial z}\right)\vec{u_r} + \left(\frac{\partial A_r}{\partial z}-\frac{\partial A_z}{\partial r}\right)\vec{u_\theta} + \frac{1}{r}\left(\frac{\partial}{\partial r}(rA_\theta)-\frac{\partial A_r}{\partial \theta}\right)\vec{u_z}
\Delta f=\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial f}{\partial r}\right) + \frac{1}{r^2}\frac{\partial^2 f}{\partial \theta^2} + \frac{\partial^2 f}{\partial z^2}

Coordonnées sphériques

\vec{\mathrm{grad}}f = \frac{\partial f}{\partial r}\vec{u_r} + \frac{1}{r}\frac{\partial f}{\partial \theta}\vec{u_\theta} + \frac{1}{r \sin\theta}\frac{\partial f}{\partial \varphi} \vec{u_\varphi}
\mathrm{div}\vec{A} = \frac{1}{r^2}\frac{\partial}{\partial r}(r^2A_r) + \frac{1}{r\sin\theta}\frac{\partial} {\partial \theta}(\sin\theta A_\theta) + \frac{1}{r\sin\theta}\frac{\partial A_\varphi}{\partial \varphi}
\vec{\mathrm{rot}}\vec{A} = \frac{1}{r\sin\theta}\left(\frac{\partial}{\partial \theta}(\sin\theta A_\varphi)-\frac{\partial A_\theta}{\partial \varphi}\right)\vec{u_r} + \left(\frac{1}{r\sin\theta}\frac{\partial A_r}{\partial \varphi}-\frac{1}{r}\frac{\partial}{\partial r}(rA_\varphi)\right)\vec{u_\theta} + \frac{1}{r}\left(\frac{\partial}{\partial r}(rA_\theta)-\frac{\partial A_r}{\partial \theta}\right)\vec{u_\varphi}
\Delta f = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial f}{\partial r}\right) + \frac{1}{r^2 \sin\theta}\frac{\partial}{\partial \theta}\left(\sin \theta\frac{\partial f}{\partial \theta}\right) + \frac{1}{r^2\sin^2\theta}\frac{\partial^2 f}{\partial \varphi^2}

Quelques formules différentielles

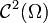
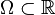
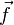
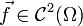
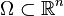
Attention : les formules suivantes sont valables à condition que certaines hypothèses soient vérifiées ! (la fonction scalaire dans la première formule doit être \mathcal{C}^2(\Omega) , où \Omega \subset \mathbb{R} , par exemple. De même, si \vec f désigne la fonction vectorielle concernée dans la seconde formule, il faut vérifier \vec f \in \mathcal{C}^2(\Omega) , \Omega \subset \mathbb{R}^n .)

  • \vec{\mathrm{rot}}(\vec{\mathrm{grad}})=\vec{0}
  • \mathrm{div}(\vec{\mathrm{rot}})=0
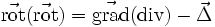
  • \vec{\mathrm{rot}}(\vec{\mathrm{rot}})=\vec{\mathrm{grad}}(\mathrm{div})-\vec{\Delta} (appliqué à un vecteur) (rotationnel du rotationnel)
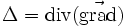
  • \Delta = \mathrm{div}(\vec{\mathrm{grad}}) (appliqué à un scalaire)

Formules dites de Leibniz pour les produits

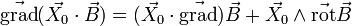
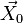
  • \vec{\mathrm{grad}}(\vec{X_0}\cdot \vec{B} ) = (\vec{X_0} \cdot \vec{\mathrm{grad}})\vec{B} + \vec{X_0} \wedge \vec{\mathrm{rot}}\vec{B} (où \vec{X_0} est un vecteur uniforme) et évidemment :
  • \vec{\mathrm{grad}}(\vec{A}\cdot \vec{B} ) = (\vec{A} \cdot \vec{\mathrm{grad}})\vec{B} + \vec{A} \wedge \vec{\mathrm{rot}}\vec{B} + (\vec{B} \cdot \vec{\mathrm{grad}})\vec{A} + \vec{B} \wedge \vec{\mathrm{rot}}\vec{A}
  • \nabla(\vec{F}\cdot \vec{F}) = 2 (\vec{F}\cdot\nabla)\vec{F} + 2 \vec{F} \wedge (\vec{\mathrm{rot}}\vec{F}) (dite de Bernoulli, en mécanique des fluides)
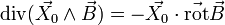
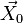
  • \mathrm{div}(\vec{X_0} \wedge \vec{B})= - \vec{X_0} \cdot \vec{\mathrm{rot}}\vec{B} (où \vec{X_0} est un vecteur uniforme, définition intrinsèque du rotationnel)
  • \mathrm{div}(\vec{A} \wedge \vec{B})= - \vec{A} \cdot \vec{\mathrm{rot}}\vec{B} + \vec{B} \cdot \vec{\mathrm{rot}}\vec{A}
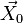
  • (où \vec{X_0} est un vecteur uniforme, par définition de l'application linéaire tangente)
  • \vec{\mathrm{rot}}( \vec{A}\wedge \vec{B}) = \vec{A}\cdot \mathrm{div}\vec{B} - (\vec{A}\cdot \vec{\mathrm{grad}})\vec{B} - \vec{B}\cdot \mathrm{div}\vec{A} + (\vec{B}\cdot \vec{\mathrm{grad}})\vec{A}
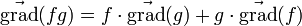
  • \vec{\mathrm{grad}}(fg) = f \cdot\vec{\mathrm{grad}}(g) + g\cdot\vec{\mathrm{grad}}(f) (symétrique en f et g)
  • \mathrm{div}(\rho \cdot \vec{V}) = \rho \cdot \mathrm{div} \vec{V}+ \vec{\mathrm{grad}}(\rho)\cdot \vec{V}
  • \vec{\mathrm{rot}}(\rho \cdot \vec{V}) = \rho \cdot \vec{\mathrm{rot}} \vec{V}+ \vec{\mathrm{grad}}(\rho)\wedge \vec{V}
  • \Delta (f\cdot g) = f\cdot \Delta g + 2 \vec{\mathrm{grad}}(f) \cdot \vec{\mathrm{grad}}(g) +g\cdot \Delta f
  • \mathrm{div} ( f \cdot \vec{\mathrm{grad}}(g) -g \cdot \vec{\mathrm{grad}}(f)) = f \Delta g - g \Delta f

Quelques formules utiles

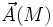
  • Soient f(M) et g(M) deux champs scalaires,il existe un champ de vecteurs \vec{A}(M) tel que :

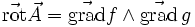
\vec{\mathrm{rot}}\vec{A} = \vec{\mathrm{grad}}f \wedge \vec{\mathrm{grad}}\,g

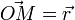
  • Le champ central \vec{OM}=\vec{r} joue un rôle très important en physique. Aussi convient-il de mémoriser ces quelques évidences :


son application linéaire tangente est la matrice identité (cf. la définition !),

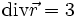
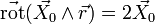
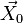
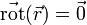
donc \mathrm{div}\vec{r}=3 et \vec{\mathrm{rot}}(\vec{X_0}\wedge\vec{r})=2\vec{X_0} (où \vec{X_0} est un vecteur uniforme) et \vec{\mathrm{rot}}(\vec{r})=\vec{0}

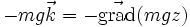
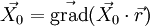
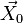
  • D'autre part -mg\vec{k}=-\vec{\mathrm{grad}}(mgz)  ; soit \vec{X_0}=\vec{\mathrm{grad}}(\vec{X_0}\cdot\vec{r}) (où \vec{X_0} est un vecteur uniforme). Et aussi:
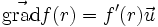
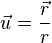
  • \vec{\mathrm{grad}}f(r)=f'(r)\vec{u} avec \vec{u}=\frac{\vec{r}}{r}

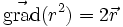
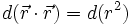
en particulier \vec{\mathrm{grad}}(r^2)=2\vec{r} (évident car d(\vec{r}\cdot\vec{r})=d(r^2) )

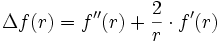
  • \Delta f(r)=f''(r)+\frac{2}{r}\cdot f'(r) , sauf en r = 0
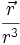
  • Le champ newtonien, soit \frac{\vec{r}}{r^3} , est très souvent étudié ,

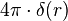
car c'est le seul champ central à divergence nulle (évident si l'on pense en termes de flux)sauf pour r = 0, où elle vaut 4\pi\cdot\delta(r)  ; ce résultat est le théorème de Gauss pour l'angle solide)

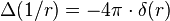
Il en résulte que \Delta(1/r) = - 4 \pi \cdot \delta(r)

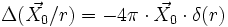
  • Donc \Delta(\vec{X_0}/r) = - 4 \pi \cdot \vec{X_0}\cdot \delta(r)

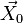
(où \vec{X_0} est un vecteur uniforme)

qui se décompose en :

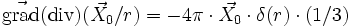
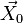
\vec{\mathrm{grad}}(\mathrm{div})(\vec{X_0}/r) = - 4 \pi \cdot \vec{X_0}\cdot \delta(r)\cdot(1/3) (où \vec{X_0} est un vecteur uniforme), et

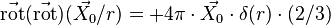
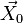
\vec{\mathrm{rot}}(\vec{\mathrm{rot}})(\vec{X_0}/r) = + 4 \pi \cdot \vec{X_0}\cdot \delta(r)\cdot(2/3) (où \vec{X_0} est un vecteur uniforme)

ce qui est moins évident (cf. moment magnétique).

  • Les formules précédentes sont dites de calcul différentiel. Il convient de les associer aux formules de calcul intégral : formule de Stokes, théorème d'Ostrogradski, etc.
  • Enfin, il convient de ne pas perdre de vue le caractère axial ou polaire des champ de vecteurs étudiés. Ce ne sont absolument pas les mêmes entités mathématiques !
Application linéaire tangente d'un champ de vecteurs
- Introduction - Principaux opérateurs différentiels linéaires de tri - Opérateurs d'ordre supérieur - Application linéaire tangente d'un champ de vecteurs - Expressions des opérateurs en différentes coordonnées - Quelques formules différentielles
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
Page générée en 0.144 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise