Axiome de séparation (topologie) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En topologie, un axiome de séparation est une propriété satisfaite par certains espaces topologiques, similaire à la propriété de séparation de Hausdorff (dite aussi T2), et concernant la séparation de points ou de fermés, en termes soit de voisinages, soit de fonctions continues réelles.
Divers axiomes de séparation peuvent être ordonnés par implication, notamment ceux de la série des axiomes codés par la lettre « T » et un indice numérique, ces axiomes étant en général d'autant plus restrictifs que les indices sont élevés et les topologies correspondantes plus fines.
Liste des axiomes
La séparation T0 (espace de Kolmogorov)
Dans un espace topologique X, deux points x et y sont dit indiscernables ssi ils appartiennent exactement aux mêmes ouverts, ou encore ssi ils ont exactement les mêmes voisinages. C'est une relation d'équivalence. On dira que X est un espace T0 lorsque les classes d'équivalence sont toutes réduites à des singletons. Autrement dit, pour deux points distincts quelconques, l'un des deux points admet un voisinage qui ne contient pas l'autre point. Un espace vérifiant cette propriété est parfois appelé espace de Kolmogorov. Le quotient de X par cette relation d'équivalence est toujours un espace de Kolmogorov.
La séparation T1 (espace accessible, ou de Frechet)
Un espace topologique X est un espace T1 ssi les singletons de X sont fermés. Ceci équivaut à : pour tout point x, l'intersection des voisinages de x est réduite au singleton {x}. Un espace est T1 si et seulement s'il est à la fois T0 et R0.
L'espace

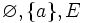
La séparation T2 (espace de Hausdorff)
C'est la propriété classique. Un espace topologique est dit T2, ou de Hausdorff, ou espace séparé, ssi pour tout couple (x,y) d'éléments distincts de X, il existe deux ouverts disjoints dont l'un contient x et l'autre contient y. Ceci équivaut à : pour tout point x, l'intersection des voisinages fermés de x est réduite au singleton {x}.
La séparation T2 entraîne la séparation T1. La réciproque est fausse : la topologie cofinie, et la topologie de Zariski sur une variété algébrique, sont T1 mais en général non séparées.
La séparation T2 1/2 (espace complètement de Hausdorff)
Un espace topologique est un espace T2 1/2 lorsque deux points distincts admettent des voisinages dont les adhérences sont disjointes. Tout espace T2 1/2 est séparé mais la réciproque est fausse, comme le montre l'exemple suivant.
On considère l'ensemble E constitué de l'intérieur du disque de centre O de rayon 1 et des deux points (1,0) et (-1,0). Une base de voisinages d'un point intérieur au disque est formée des disques centrés en ce point. Une base de voisinages du point (1,0) est constituée des ouverts réunion de ce point et d'une bande semi-circulaire (ouverte) adjacente à ce point et limitée par des segments [(0,1), (0,1-h)] et [(0,-1), (0,-1+h)]. De même pour (-1,0). Dans le dessin ci-dessous, on a représenté en couleur un voisinage d'un point intérieur au disque, et un voisinage de chacun des points (1,0) et (-1,0). Si ces deux derniers voisinages sont ouverts, ils sont disjoints, mais leurs adhérences s'intersectent selon une partie des segments communs qui les limitent. L'espace E est donc séparé mais pas T2 1/2.
La séparation T2 3/4 (espace d'Urysohn)
Un espace topologique X est appelé espace d'Urysohn lorsque pour tous points distincts a et b de X, il existe une fonction continue f de X dans le segment [0,1] telle que f(a)=0 et f(b)=1. Un espace d'Urysohn vérifie T2 1/2.
Un espace est Urysohn ssi l'application canonique vers son compactifié de Stone-Cech est injective.
La séparation T3 + (espace régulier)
Un espace topologique X vérifie T3 lorsque pour tout point a de X et pour tout fermé F de X ne contenant pas a, il existe deux ouverts disjoints dont l'un contient a et l'autre contient F.
On remarquera qu'un espace peut vérifier T3 sans être séparé : la topologie grossière vérifie T3. Par contre si X vérifie T3 et T0 alors il est séparé.
Un espace séparé vérifiant T3 est appelé espace régulier.
Un tel espace vérifie T2 1/2, mais pas toujours T2 3/4.
La séparation T3 1/2 + (espace complètement régulier, ou de Tychonov)
Un espace topologique X vérifie T3 1/2 ssi pour tout point a de X et pour tout fermé F de X ne contenant pas a, il existe une fonction continue de X dans le segment [0,1] valant 0 en a et 1 sur F. Ceci équivaut à : X est uniformisable.
On remarquera qu'un espace peut être uniformisable sans être séparé : la topologie grossière vérifie T3 1/2. Par contre si X vérifie T3 1/2 et T0 alors il est séparé.
Un espace séparé vérifiant T3 1/2 est qualifié de complètement régulier (on dit aussi espace de Tychonov).
Un espace X est complètement régulier ssi X est homéomorphe à un sous-espace d'un espace compact C. Dans ce cas, C peut être choisi égal au compactifié de Stone-Cech de X (muni de l'application canonique de X dans C).
Un espace complètement régulier est donc non seulement régulier mais aussi d'Urysohn.
La séparation T4 + (espace normal)
Un espace topologique X vérifie T4 lorsque pour tout couple de fermés disjoints F1 et F2, il existe un couple d'ouverts disjoints dont l'un contient F1 et l'autre contient F2.
Cet axiome n'est pas préservé par sous-espaces ni par produits. On a seulement : si X vérifie T4 alors tout sous-espace fermé de X vérifie T4.
Cet axiome n'implique aucun des précédents. En particulier, un espace peut vérifier T4 sans être séparé : la topologie grossière vérifie T4. Par contre si un espace vérifie T4 et T1 alors il est séparé.
Un espace séparé vérifiant T4 est qualifié de normal.
Dans un espace normal, pour tout couple de fermés disjoints F1 et F2, il existe une fonction continue de X dans le segment [0,1] valant 0 sur F1 et 1 sur F2. Cette propriété remarquable s'appelle lemme d'Urysohn.
En particulier, tout espace normal est complètement régulier.
Tout espace topologique compact est normal.
La séparation T5 + (espace complètement normal)
Un espace topologique X vérifie T5 ssi pour toutes parties A et B de X telles que
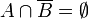
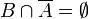
Ceci équivaut à : tout sous-espace de X vérifie T4.
- Premièrement l'implication ; soient X vérifiant T5 et Y un sous-espace de X. Alors Y vérifie T5 (donc T4). En effet, pour toutes parties A et B de Y, l'adhérence de B dans le sous-espace Y (muni de sa topologie induite) est égale à
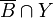
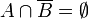
- Ensuite la réciproque ; soit X un espace topologique dont tous les sous-espaces vérifient T4. Soient A et B deux parties de X telles que
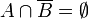
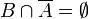
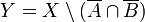


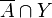
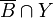
Un espace séparé vérifiant T5 est qualifié de complètement normal.
Un espace est donc complètement normal ssi tous ses sous-espaces sont normaux.
La séparation T5 1/2 (espace parfaitement normal)
Un espace séparé X est dit parfaitement normal ssi tout fermé de X est le lieu d'annulation d'une application continue f de X dans R.
Tout espace métrisable est parfaitement normal (prendre pour f la fonction distance au fermé).
Tout sous-espace d'un espace parfaitement normal est encore parfaitement normal.
Un espace parfaitement normal est normal (et par suite complètement normal, d'après la stabilité précédente pour les sous-espaces). Mieux : pour tous fermés disjoints F1 et F2 d'un tel espace X, f1 et f2 étant des fonctions continues qui s'annulent exactement sur ces fermés, la fonction
![\frac{|f_1|}{|f_1|+|f_2|}:X\to[0,1]](https://static.techno-science.net/illustration/Definitions/autres/c/caec7056d70e6942baf1fabadef9cb07_32a8e823fb081329c65e4aa48bd3b7e1.png)
La définition originelle (due à Čech et équivalente) est : un espace est parfaitement normal ssi il est normal et chacun de ses fermés est un Gδ, c'est-à-dire une intersection dénombrable d'ouverts (en l'occurrence
![\bigcap_{n=1}^{+\infty}f^{-1}\left(\,\left]-1/n,1/n\right[\,\right)](https://static.techno-science.net/illustration/Definitions/autres/4/4dcc28be5babf6d32d742b019583c51e_5a106e3aed7df94caa895a65490df2d7.png)
Attention : dans la littérature, le vocabulaire est parfois très volatil et certaines de ces définitions peuvent être interchangées.



















































