Compacité (mathématiques) - Définition

En topologie de la droite réelle, la propriété de Borel-Lebesgue est une propriété topologique remarquable des segments, basée sur la notion de recouvrement. Elle sert d'axiome en topologie générale pour définir la notion d'espace compact, et étendre plusieurs des résultats concernant les segments à un cadre très général. Le nom choisi pour cet axiome rend hommage aux mathématiciens français Émile Borel et Henri Lebesgue.

Propriété de Borel-Lebesgue

Définition préalable : Soit E un ensemble, et A une partie de E. On dit qu'une famille de parties de E recouvre A si leur réunion contient A

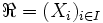
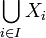
Propriété de Borel-Lebesgue pour les segments : soit un segment [a,b] de la droite réelle. De tout recouvrement de ce segment par des ouverts, on peut extraire un sous-recouvrement fini. C'est-à-dire que pour toute famille d'ensembles ouverts recouvrant [a,b], il existe une partie finie J de I telle que la sous-famille recouvre [a,b].

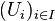
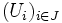
Pour une démonstration de cette propriété voir le théorème de Borel-Lebesgue, aussi appelé théorème de Heine-Borel.

La propriété de Borel-Lebesgue est étroitement liée à une propriété des suites bornées de réels : de toute suite bornée de réels, on peut extraire une suite convergente. Le lien entre les deux propriétés apparaîtra plus nettement dans la section suivante.

De l'une ou l'autre de ces propriétés il est possible de tirer quelques conséquences importantes sur les fonctions numériques. Notamment : l'image d'un segment par une application continue est un segment, et la fonction est alors uniformément continue (théorème de Heine).

Axiome de Borel-Lebesgue et définition générale des compacts

Un espace topologique E est dit quasi-compact s'il vérifie l'axiome de Borel-Lebesgue : de tout recouvrement ouvert de E, on peut extraire un sous-recouvrement fini. L'espace est dit compact quand il est en outre séparé.

Par passage au complémentaire, cette dernière propriété est équivalente à la propriété suivante : si est une famille de fermés telle que , alors on peut extraire une famille finie , avec , telle que . Ou encore, par contraposition, si toute intersection finie d'une famille de fermés est non vide, alors l'intersection de toute la famille est non vide.

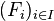
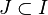
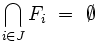
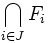
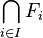
NB : La terminologie anglo-saxonne demande seulement la propriété des sous-recouvrements finis mais pas nécessairement la séparation.

Propriétés : compacts et fermés

Toute partie compacte d'un espace topologique séparé est fermée.

Démontrons cette propriété par contraposition. Soit A un espace qui n'est pas fermé. Alors il existe un point b adhérent à A et qui n'est pas élément de A. Si ce n'était pas le cas A serait égal à son adhérence qui est par définition fermée. Pour chaque point a de A, il existe alors un ouvert O_a contenant a et un ouvert B_a contenant b tel que leurs intersection est vide, car l'espace est séparé. L'ensemble des O_a forment un recouvrement ouvert de A. Et tout recouvrement fini extrait ne rencontre pas l'intersection des B_a associés. Or cette intersection finie est un ouvert (car il est défini comme une intersection finie d'ouverts) contenant b. Elle possède une intersection non vide avec A car tout voisinage d'un point adhérent à un ensemble rencontre cet ensemble. Et A n'est pas compact.

NB: Ceci est en général faux si l'espace ambiant n'est pas séparé ; par exemple dans munie de la topologie grossière , est compact mais pas fermé.

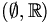
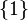
Toute partie fermée d'un espace compact est compacte

Soit C un espace compact, F une partie fermée de C, et un recouvrement ouvert de F. Si l'on adjoint à l'ensemble ouvert C − F, on obtient un recouvrement ouvert de C. Puisque C est compact, on peut extraire de un recouvrement fini de C. Comme est un recouvrement de C c'est aussi un recouvrement de F. Hormis l'éventuel ensemble C − F, tous les membres de sont par construction membres de , recouvrement d'origine de F. En en enlevant C − F, qui ne contribue pas à recouvrir F, on obtient un recouvrement fini de F extrait du recouvrement d'origine .

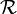
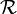
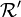
Théorème de Bolzano-Weierstrass et compacité séquentielle

Dans le cadre des espaces métriques (automatiquement séparés), le théorème de Bolzano-Weierstrass énonce qu'un espace K est compact si et seulement si de toute suite d'éléments de K il est possible d'extraire une sous-suite qui converge vers un élément de K.

Pour cette raison, dans le cadre des espaces métriques, la propriété de compacité est fréquemment introduite par caractérisation séquentielle.