Bouteille de Klein - Définition

Introduction

vue de la bouteille de Klein dans un espace à trois dimensions.

En mathématiques, la bouteille de Klein (prononcer « klaïn ») est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle il n'est pas possible de définir un « intérieur » et un « extérieur ». La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein. Elle est étroitement liée au ruban de Möbius et a des prolongements du plan projectif réel tels que la surface de Boy.

C'est un des exemples les plus simples de variété abstraite, car c'est une surface qui ne peut être représentée convenablement dans l'espace à trois dimensions. Mathématiquement, on dit qu'elle possède une immersion de classe dans l'espace de dimension trois, mais n'y possède pas de plongement continu.

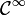
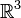
Construction

La bouteille de Klein n'est possible à représenter dans l'espace (l'espace à 3 dimensions), que si l'on accepte qu'elle se traverse elle-même ; aussi, aucune réalisation que l'on peut voir de la bouteille de Klein n'est « exacte ». Dans , il est par contre possible de la réaliser sans auto-intersection (mathématiquement, on dit qu'elle possède un plongement (immersion injective) de classe dans ).

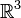
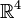
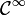
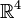
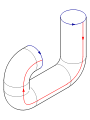
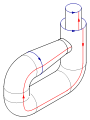
Voici un plan de montage dans . À partir du carré initial, on colle les deux bords rouges l'un contre l'autre, dans le sens des flèches. La figure obtenue est un cylindre, dont on veut identifier les deux bords à l'aide des flèches bleues. Pour respecter le sens de ces flèches, il est nécessaire de retourner l'un des cercles avant de le recoller à l'autre, et pour cela, d'opérer une auto-intersection.

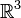
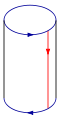
Si les deux segments bleus étaient orientés de la même façon, le recollement des segments opposés donnerait un tore. Si au contraire, les deux segments rouges étaient orientés en sens inverse comme les deux segments bleus, le recollement des segments opposés donnerait un plan projectif.

Construction alternative

La bouteille de Klein peut aussi être obtenue par recollement de deux rubans de Möbius le long de leurs bords.

On se donne deux exemplaires d'un tel carré, et on obtient deux exemplaires de ruban de Möbius en faisant cette fois d'abord l'identification suivant les flèches bleues. Chacun de ces rubans a alors un seul bord : les côtés verticaux rouges qui ont été connectés suite à l'identification précédente ; recoller les deux rubans suivant leurs bords peut alors être considéré comme équivalent à recoller le bord droit du second carré, au bord gauche du premier, et vice-versa. On voit aisément qu'on retrouve alors bien le cylindre, mais avec l'identification des bords bleus déjà effectuée, c'est-à-dire la bouteille de Klein.

On peut imaginer le plan de montage comme ça...

Bouteille de Klein séparée selon son plan de symétrie en deux bandes de Möbius

Il est peut-être plus facile de voir qu'une bouteille de Klein coupée en deux dans le sens de la hauteur fournit bien deux rubans de Möbius.