Cylindre - Définition

Introduction

Un exemple de cylindre de révolution

Un cylindre est une surface dans l'espace définie par une droite (d), appelée génératrice, passant par un point variable décrivant une courbe plane fermée (c), appelée courbe directrice et gardant une direction fixe. On parle aussi de surface cylindrique.

On peut considérer un cylindre comme un cône dont le sommet est « rejeté à l'infini ».

Par extension, on appelle encore cylindre le solide délimité par une surface cylindrique et par deux plans strictement parallèles. Si ces plans sont perpendiculaires à la droite génératrice, on dit que le cylindre est droit. La distance séparant les deux plans parallèles s'appelle la hauteur du cylindre et la surface délimitée par la courbe directrice s'appelle la base du cylindre. Si on note H la hauteur du cylindre et A l'aire de sa base, alors son volume V est donné par l'égalité : V = A × H. Les prismes (dont les cubes et les parallélépipèdes rectangles) sont des cas particuliers de cylindre. Mais (sauf mention spéciale) on réserve généralement ce terme aux cylindres de révolution, dont la base est un cercle.

Cylindre de révolution

Un cylindre de révolution, appelé aussi cylindre circulaire droit, est un cylindre dont la courbe directrice est un cercle et dont la droite génératrice est perpendiculaire au plan contenant le cercle directeur.

Dans l'espace rapporté au repère orthonormal , le cylindre d'axe a pour équation : où est le rayon du cercle directeur.

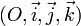
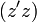
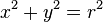
Note : la plupart des gens pensent que le terme cylindre s'applique exclusivement au cylindre de révolution.

Cylindre en volume

Il existe une définition mathématique plus formelle du cylindre, qui inclut tous les points internes. Cette définition est généralisable à n dimensions d'un espace euclidien. Dans , le cylindre de révolution et de rayon R, d'axe , est défini par :

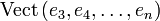
Mécanique

• Les cylindres sont les parties qui guident le mouvement des pistons dans différents dispositifs basés sur la différence de pression entre 2 zones :
  • système pneumatique :
    • Cylindre d'un moteur à piston
    • Cylindre de machine à vapeur
  • Système hydraulique :
    • Cylindre émetteur et récepteur de frein hydraulique

• Cylindre de sécurité de serrure

• Le terme cylindrée qui est dérivé du mot cylindre, s'applique par extension à toutes les chambres fermées abritant le mouvement d'un piston, quelle que soit leur forme.