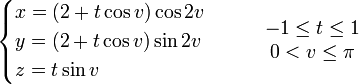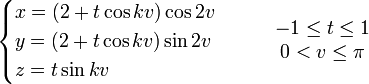Ruban de Möbius - Définition

Introduction

Réalisation à partir d'une bande de papier

En topologie, le ruban de Möbius (aussi appelé bande de Möbius ou anneau de Möbius) est une surface fermée dont le bord est homéomorphe à un cercle. Autrement dit, il ne possède qu'une seule face contrairement à un ruban classique qui en possède deux. Elle a la particularité d'être réglée et non-orientable. Cette surface a été décrite indépendamment en 1858 par les mathématiciens August Ferdinand Möbius (1790-1868) et Johann Benedict Listing (1808-1882). Le nom du premier fut retenu grâce à un mémoire présenté à l'Académie des sciences à Paris. On trouve également les dénominations de bande, anneau ou ceinture de Möbius ou, abusivement et phonétiquement, de Moebius, notamment dans les traductions.

Il est facile de visualiser la bande de Möbius dans l'espace : un modèle simple se réalise en faisant subir une torsion d'un demi-tour à une longue bande de papier, puis en collant les deux extrémités. Si l'on coupe le ruban en deux dans le sens de la longueur, on obtient un anneau unique, vrillé, mais qui possède deux faces distinctes et deux bords distincts.
Si on le recoupe dans le sens de la longueur, on obtient... deux anneaux distincts, vrillés et entortillés l'un sur l'autre.

Définition par torsion d'une bande dans l'espace

Plan de montage du ruban

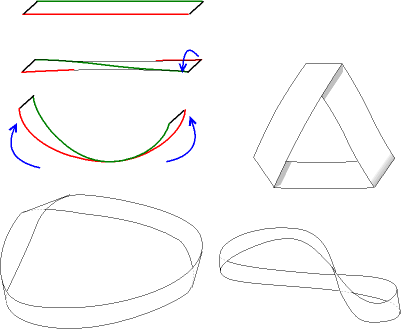
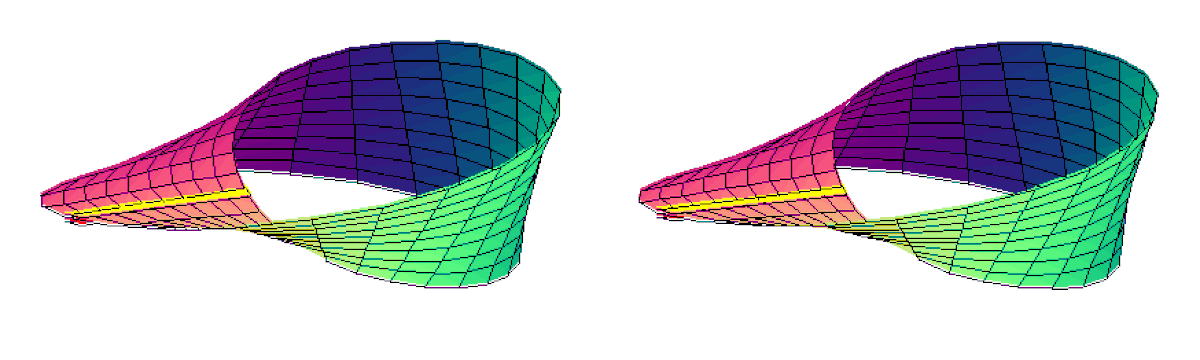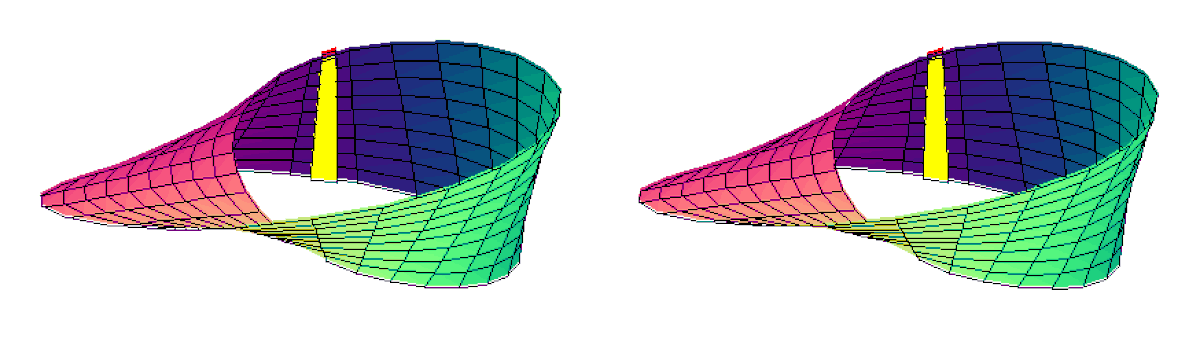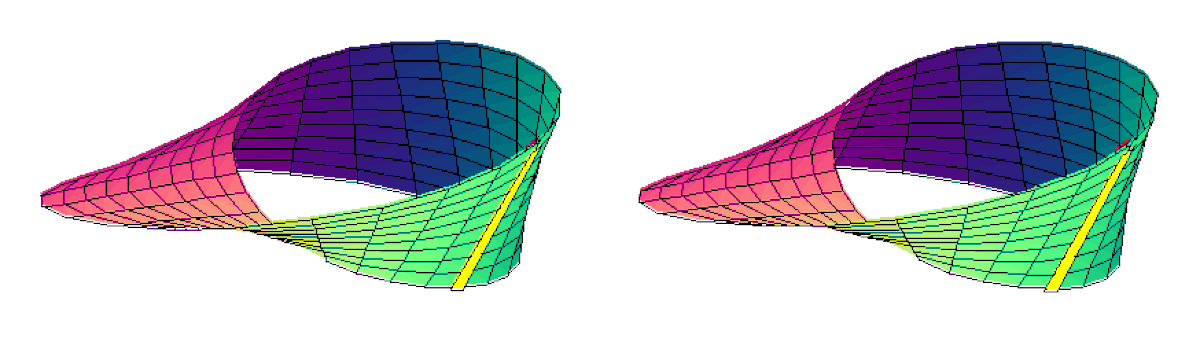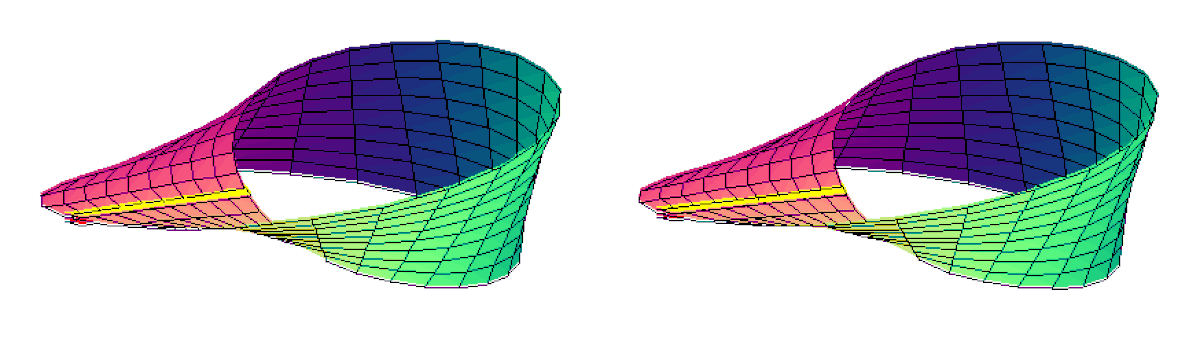
Confection du ruban	Schématisation du montage : recoller les deux flèches en respectant le sens

Ruban de Möbius classique

Le ruban de Möbius peut être engendré par un segment pivotant dont le centre décrit un cercle fixe. Un paramétrage correspondant est

Les courbes v = v₀, t variant seul, sont bien des segments, reliant à vitesse uniforme le point v = v₀, t = - 1 et le point v = v₀, t = 1. Ce segment est donc de longueur 2.

La courbe t = 0 est un cercle de rayon 2 dans le plan horizontal ; elle représente la trajectoire du centre des segments. L'angle que fait le segment avec la direction horizontale est v₀. Lorsque le centre a fait un tour complet sur le cercle horizontal (ajout de π à la variable v), le segment a fait un demi-tour seulement. Ce qui provoque le raccordement par exemple du point t = 1, v = π avec t = - 1, v = 0.

Le bord du ruban est donné par la courbe t = 1 ou t = - 1. Mais c'est la même courbe : le bord du ruban de Möbius est en un seul morceau (connexe).

On peut également voir l'animation ci-dessus en vision stéréoscopique :

• Animation stéréoscopique croisée :
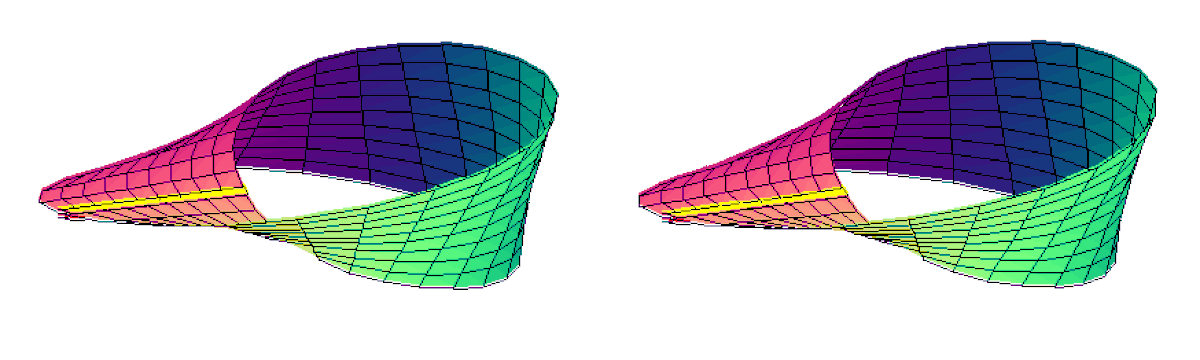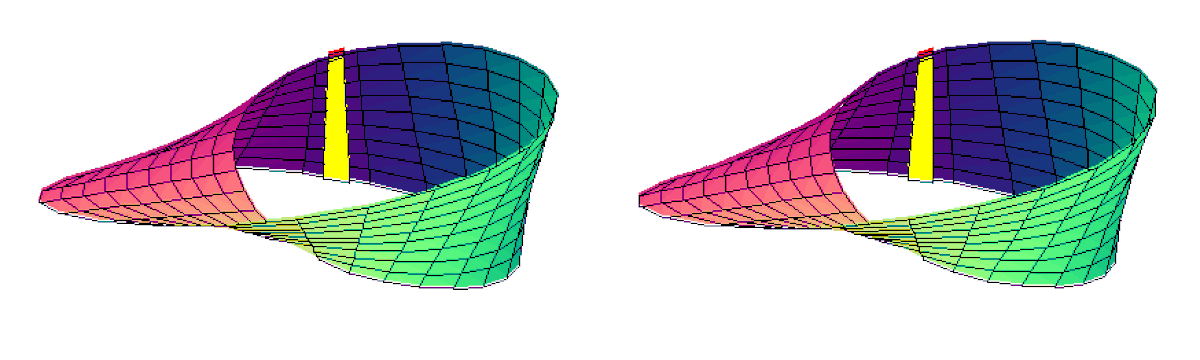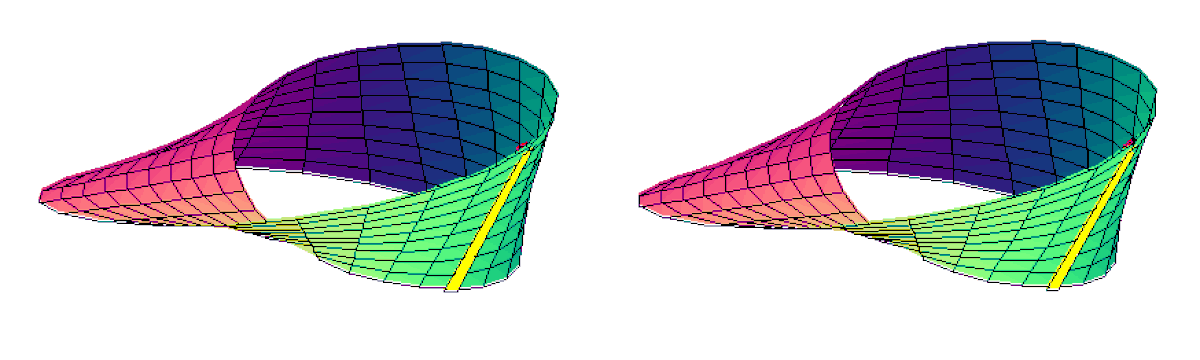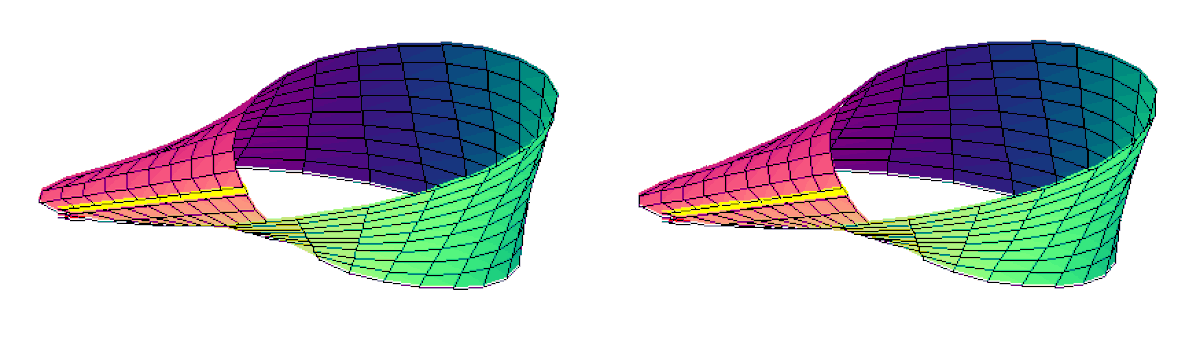
• Animation stéréoscopique parallèle du même ruban :
• Les deux animations regroupées sur une même animation :

Autres figures obtenues par torsion

Des variantes du ruban classique peuvent s'obtenir en faisant subir à la bande de papier un nombre impair de demi-tours de sens direct ou rétrograde. Il suffit d'ajuster le paramétrage précédent :

avec entier relatif impair.

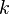
Les figures obtenues pour k et -k sont énantiomorphes, c'est-à-dire des images miroirs l'une de l'autre.

Si l'on accepte des valeurs paires de k on obtient des rubans à deux faces, plus ou moins entortillés.

Comparaison des différents rubans

On peut s'intéresser à la courbe formant le bord de ces rubans. Elle a un entortillement différent pour chaque valeur de k. L'entortillement se calcule par exemple en projection (vue de dessus), en comptant le nombre de fois où la courbe passe au-dessus d'elle-même. On ne peut déformer continûment (c'est-à-dire par homotopie) un type de ruban en un autre dans l'espace de dimension 3.

Pourtant les différents rubans sont homéomorphes au ruban de Möbius classique, c’est-à-dire qu'il n'y a pas de différence intrinsèque entre eux. Celle-ci est liée à la façon dont ils sont plongés dans l'espace de dimension 3.

Le ruban de Möbius à un demi-tour peut également être vu comme une partie de la surface de Möbius.

Objets dérivés

Si on colle deux rubans de Möbius le long de leur bord, on obtient une bouteille de Klein.

Si on colle un disque à un ruban de Möbius le long de leur bord, on obtient une surface de Boy.