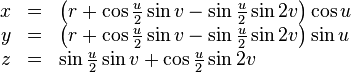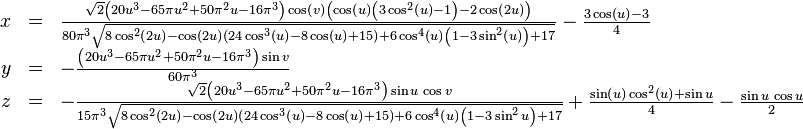Bouteille de Klein - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Construction - Paramétrisation - Visualisation - Origine du nom - Propriétés - Références dans la culture populaire

Paramétrisation

L'immersion « 8 » de la bouteille de Klein

La « figure 8 » qui correspond à une immersion de la bouteille de Klein admet une paramétrisation simple :

\begin{array}{rcl} x & = & \left(r + \cos\frac{u}{2}\sin v - \sin\frac{u}{2}\sin 2v\right) \cos u\\ y & = & \left(r + \cos\frac{u}{2}\sin v - \sin\frac{u}{2}\sin 2v\right) \sin u\\ z & = & \sin\frac{u}{2}\sin v + \cos\frac{u}{2}\sin 2v \end{array}

Dans cette immersion, l'auto-intersection est un cercle inscrit dans le plan XY. La constante positive $r$ est le rayon de ce cercle. Le paramètre $u$ donne l'angle dans le plan XY et $v$ spécifie la position par rapport à la section de la figure (une tranche qui forme un 8).

La paramétrisation de l'immersion dans trois dimensions de la bouteille de Klein elle-même est plus complexe. Dans la version simplifiée ci-dessous, $u$ est un paramètre qui suit le corps de la bouteille tandis que $v$ évolue le long de sa section.

\begin{array}{rcl} x & = & \frac{\sqrt{2}\left( 20u^{3}-65\pi u^{2}+50\pi^{2}u-16\pi^{3}\right)\cos \left(v\right) \left(\cos \left(u\right)\left(3\cos^{2}\left(u\right)-1 \right)-2\cos\left(2u\right)\right)}{80\pi^{3}\sqrt{8\cos^{2}\left(2u\right)-\cos\left(2u\right)\left(24\cos^{3}\left(u\right)-8\cos\left(u\right)+15\right)+6\cos^{4}\left(u\right)\left(1-3\sin^{2}\left(u\right)\right)+17}}-\frac{3\cos \left(u\right)-3}{4}\\ y & = & -\frac{\left(20u^{3}-65\pi u^{2}+50\pi^{2}u-16\pi^{3}\right)\sin v}{60\pi^{3}}\\ z & = & -\frac{\sqrt{2}\left(20u^{3}-65\pi u^{2}+50\pi^{2}u-16\pi^{3}\right)\sin u \,\cos v}{15\pi^{3}\sqrt{8\cos^{2}\left(2u\right)-\cos\left(2u\right)\left(24\cos^{3}\left(u\right)-8\cos\left(u\right)+15\right)+6\cos^{4}\left(u\right)\left(1-3\sin^{2}u\right)+17}}+\frac{\sin \left(u\right) \cos^{2} \left(u\right)+\sin u}{4}-\frac{\sin u\,\cos u}{2} \end{array}

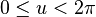
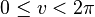
avec $0\le u<2\pi$ et $0\le v<2\pi$ .

Visualisation

Réalisation de l'immersion de la bouteille de Klein, en verre

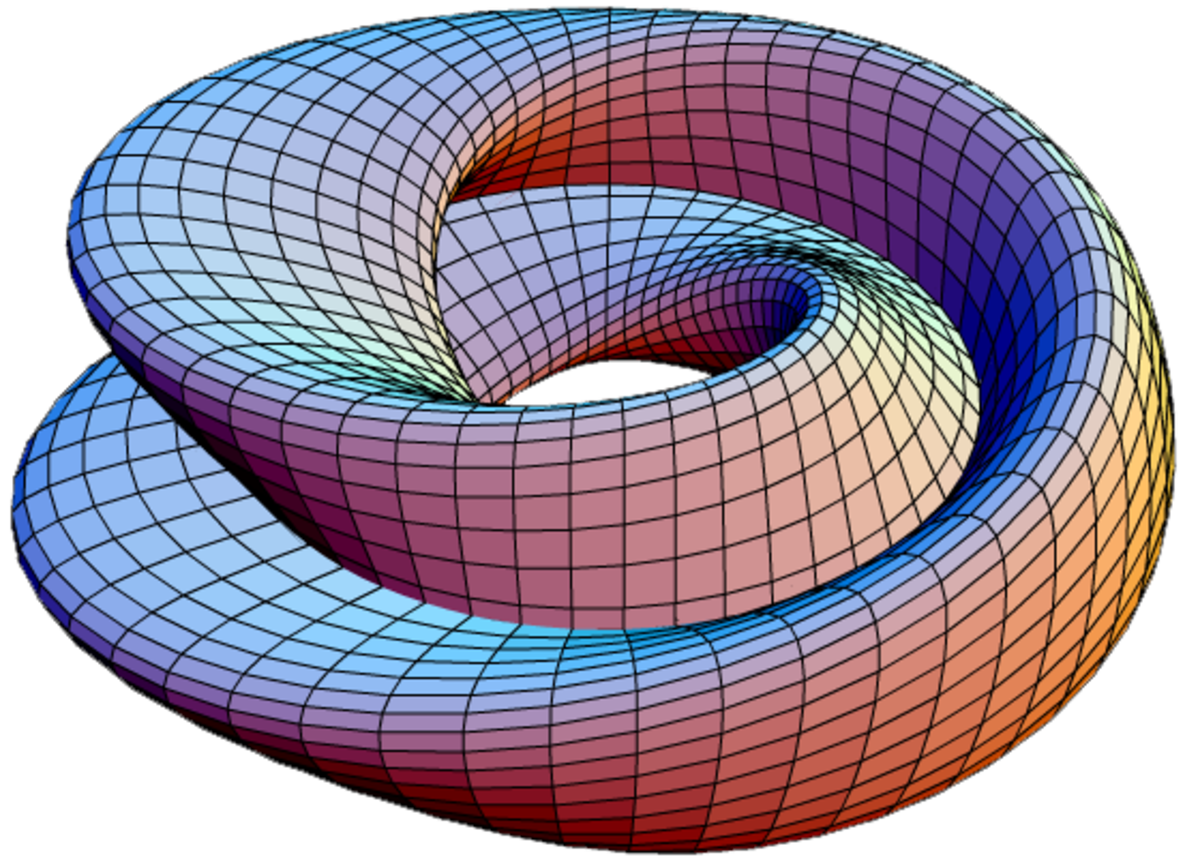
Il est possible de comprendre la structure de la bouteille de Klein à partir de la représentation fournie dans cet article, et au prix d'un effort intellectuel moins important que ce que l'on pourrait croire.

Imaginons un individu vivant dans un monde plat, à 2 dimensions. On essaye alors d'expliquer à l'individu ce qu'est un nœud. Pour cela, on lui dessine un nœud sur le plan : il ne voit qu'une courbe qui s'auto-intersecte. On lui explique alors que ce ne sont pas des points d'intersections qu'il voit, mais que la courbe passe « dessus » et « dessous ». Notre individu est interloqué : vivant dans un monde plat, il ne comprend pas ce qu'est le dessus ni ce qu'est le dessous. Il lui manque une dimension (le haut et le bas) pour pouvoir visualiser le nœud.

Nous rencontrons le même problème lorsque nous essayons de visualiser la bouteille de Klein, puisque nous voyons une surface qui s'auto-intersecte. Néanmoins, si nous raisonnons avec une quatrième dimension, il suffit d'imaginer qu'à cet endroit, la bouteille passe « dessus » et « dessous » au sens de cette quatrième dimension, et donc ne s'auto-intersecte pas.

On peut en quelque sorte considérer que la bouteille de Klein est une surface qui fait un « nœud ». En tant que surface (objet à 2 dimensions), il lui faut 4 dimensions pour faire un nœud, de même que pour une courbe (objet à une dimension) il faut 3 dimensions pour faire un nœud.

Musée du quai Branly

Dans le musée du quai Branly, l'image de la bouteille de Klein est explicitement citée dans un panneau pour expliquer la vision de la sexualité dans les civilisations dites primitives. L'homme parfait est perçu comme un individu dont les parties reproductives se confondent avec l'intérieur de la bouche si bien que cet homme n'a ni intérieur ni extérieur. Pour appuyer le discours, le visiteur peut remarquer la présence de la bouteille de Klein produite en verre comme ci-dessus au milieu de statuettes primitives.

Origine du nom

Le nom de la surface, « bouteille de Klein », provient en fait d'une erreur de traduction de l'expression allemande Kleinsche Fläche (« surface de Klein »). Il y a eu en effet une confusion entre Fläche (« surface ») et Flasche (« bouteille »). Cependant, le terme fautif s'est imposé, y compris en allemand, où l'on utilise maintenant le terme Kleinsche Flasche (« bouteille de Klein »). 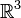Il faut dire que l'immersion de la surface de Klein dans $\mathbb R^3$ ressemble un peu à une bouteille !