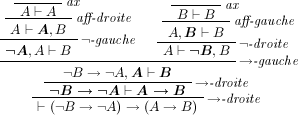Calcul des séquents - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En logique mathématique et plus précisément en théorie de la démonstration, le calcul des séquents est un système de déduction créé par Gerhard Gentzen.
Le nom de ce formalisme fait référence à un style particulier de déduction qui manipule des séquents ; le système original a été adapté à diverses logiques, telles que la logique classique, la logique intuitionniste et la logique linéaire.
Un séquent est une suite d'hypothèses suivie d'une suite de conclusions, les deux suites étant usuellement séparées par le symbole
Historique et motivation
En 1934 Gentzen a proposé la déduction naturelle, un formalisme pour décrire les preuves du calcul des prédicats, dont l'idée était de coller au plus près à la manière dont les mathématiciens raisonnent. Il a ensuite tenté d'utiliser la déduction naturelle pour produire une preuve syntaxique de la cohérence de l'arithmétique, mais les difficultés techniques l'ont conduit à reformuler le formalisme en une version plus symétrique : le calcul des séquents. C'est dans ce cadre qu'il a démontré ce qui devait devenir l'un des théorèmes principaux de la théorie de la démonstration : le théorème d'élimination des coupures. Dag Prawitz a montré en 1965 que ce théorème pouvait se transporter à la déduction naturelle.
Théorème d'élimination des coupures
Aussi connu sous le nom de «théorème de Gentzen» ou « Hauptsatz » (parce que c'était le théorème principal des deux articles fondateurs de Gentzen), ce théorème énonce que toute démonstration en calcul des séquents peut être transformée en une démonstration de même conclusion, mais qui n'utilise pas la règle de la coupure.
La démonstration de Gentzen fournit un algorithme qui, appliqué à une démonstration quelconque, aboutit à une démonstration sans coupures du même séquent conclusion.
Rasiowa et Sikorski ont publié en 1959 une preuve sémantique du théorème de Gentzen pour le cas classique, qui montre l'existence de la démonstration sans coupures, mais ne donne pas un procédé (de normalisation) qui y conduit étape par étape.
Définition
On donne ici une version légèrement modernisée par rapport à celle de Gentzen du calcul des séquents LK qui formalise la logique classique. On verra plus bas que sur le même principe on peut définir LJ, un calcul des séquents pour la logique intuitionniste, LL pour la logique linéaire... La définition ci-dessous suppose un minimum de familiarité avec le calcul des prédicats.
Note terminologique
Le terme calcul des séquents est une traduction de l'anglais sequent calculus, lui-même hérité de l'allemand Sequenzenkalkül. La traduction littérale de l'allemand en français donnerait plutôt calcul des séquences et on trouve certains auteurs utilisant cette terminologie. Toutefois l'usage le plus courant a imposé l'emploi du néologisme séquent.
Séquent
L'objet de base du calcul est le séquent, qui est un couple de listes finies (éventuellement vides) de formules. Les séquents sont usuellement notés :
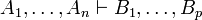
où les Ai sont les hypothèses et les Bj sont les conclusions du séquent. On voit ici apparaître l'innovation majeure du calcul des séquents : la symétrie parfaite entre hypothèses et conclusions. Un autre point important à noter est qu'une même formule peut apparaître plusieurs fois à gauche et/ou à droite dans un séquent, par exemple A1 peut être la même formule que An ; on dit alors que cette formule a plusieurs occurrences dans le séquent.
Interprétation d'un séquent
La notation séquent peut se comprendre comme une astuce syntaxique pour dénoter des formules particulières ; la virgule à gauche s'interprète comme une conjonction, la virgule à droite comme une disjonction et le symbole
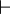
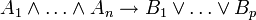
Lorsque que la liste d'hypothèses est vide on peut l'interpréter comme le vrai (c'est-à-dire l'élément neutre de la conjonction) et lorsque la liste de conclusions est vide on peut l'interpréter comme le faux (c'est-à-dire l'élément neutre de la disjonction).
Règles
Les règles sont de la forme :
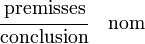
Les règles du calcul des séquents spécifient comment à partir d'un certain nombre (éventuellement nul) de séquents prémisses, on peut dériver un nouveau séquent conclusion. Dans chacune des règles les lettres grecques Gamma, Delta, etc. dénotent des suites de formules, on fait figurer les séquents prémisses au-dessus, séparés par un trait horizontal du séquent conclusion. Elles se divisent en trois groupes : le groupe identité, le groupe structurel et le groupe logique.
Groupe identité
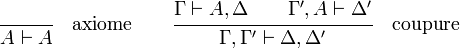
Une discussion sur la règle de coupure figure plus bas. Remarquons que la règle axiome est la seule de tout le calcul qui n'a pas de séquent prémisse.
Pour les groupes structurel et logique, les règles viennent par paire selon le côté, gauche ou droit, du séquent où elles agissent.
Groupe structurel
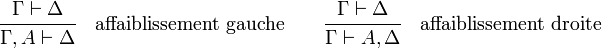
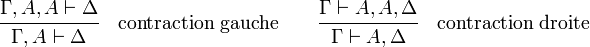
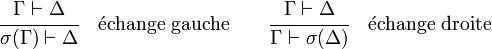
Dans les règles d'échange la notation σ(Γ) désigne une permutation des (occurrences de) formules figurant dans Γ. Les règles d'échanges sont responsables de la commutativité de la logique.
Les règles de contraction et d'affaiblissement expriment une forme d'idempotence des opérateurs «


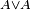
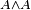
Groupe logique
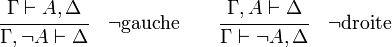
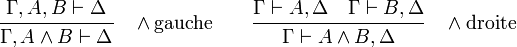
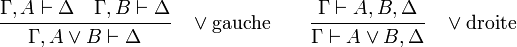
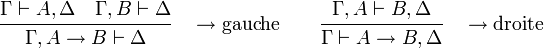
![\cfrac {\Gamma,A[t/x] \vdash \Delta} { \Gamma,\forall x\cdot A \vdash \Delta} \quad \forall\mathrm{ gauche} \qquad \cfrac {\Gamma \vdash A,\Delta} {\Gamma \vdash \forall x\cdot A,\Delta } \quad \forall\mathrm{ droite}](https://static.techno-science.net/illustration/Definitions/autres/f/f6c4054b7f605963f893c26127ee60c8_019b31ef8b9b1bc73fdfd0803a774590.png)
![\cfrac {\Gamma,A \vdash \Delta} { \Gamma,\exists x\cdot A \vdash \Delta} \quad \exists\mathrm{ gauche} \qquad \cfrac {\Gamma \vdash A[t/x],\Delta} {\Gamma \vdash \exists x\cdot A,\Delta } \quad \exists\mathrm{ droite}](https://static.techno-science.net/illustration/Definitions/autres/7/71b958c3fb587a70a0cbc8a816e7ee82_26ad352155aabdffd21146f2b34f3656.png)
Les règles de quantificateurs sont soumises à des restrictions : dans les règles de

Démonstrations
Une démonstration de LK est un arbre de séquents construit au moyen des règles ci-dessus de façon à ce que chaque séquent soit conclusion d'exactement une règle ; la démonstration est terminée si l'on arrive à ce que toutes les feuilles de l'arbre soient des règles axiome. Le séquent racine de l'arbre est la conclusion de la démonstration. Voici un exemple de démonstration du principe de contraposition de l'implication ; pour simplifier on a omis les utilisations de règles d'échange et représenté en gras les (occurrences de) formules dans les séquents prémisses sur lesquelles porte chaque règle :