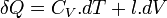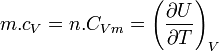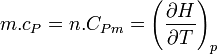Capacité thermique - Définition et Explications

Introduction

La capacité thermique (ou capacité calorifique) d'un corps est une grandeur permettant de quantifier la possibilité qu'a un corps d'absorber ou restituer de l'énergie par échange thermique au cours d'une transformation pendant laquelle sa température (La température est une grandeur physique mesurée à l'aide d'un thermomètre et...) varie. La capacité thermique (La capacité thermique (ou capacité calorifique) d'un corps est une grandeur permettant de...) est l'énergie (Dans le sens commun l'énergie désigne tout ce qui permet d'effectuer un travail, fabriquer de la...) qu'il faut apporter à un corps pour augmenter sa température de un Kelvin (Le kelvin (symbole K, du nom de Lord Kelvin) est l'unité SI de température thermodynamique. Par...). Elle s'exprime en Joule/Kelvin. C'est une grandeur extensive : plus la quantité de matière (La quantité de matière est une grandeur de comptage d'entités chimiques ou physiques...) est importante plus la capacité thermique (La thermique est la science qui traite de la production d'énergie, de l'utilisation de...) est grande. Toutes choses étant égales par ailleurs, plus la capacité thermique d'un corps est grande, plus grande sera la quantité (La quantité est un terme générique de la métrologie (compte, montant) ; un scalaire,...) d'énergie échangée au cours d'une transformation s'accompagnant d'une variation de la température de ce corps.

Histoire

Avant le développement de la thermodynamique (On peut définir la thermodynamique de deux façons simples : la science de la chaleur...) moderne, on pensait que la chaleur (Dans le langage courant, les mots chaleur et température ont souvent un sens équivalent :...) était un fluide (Un fluide est un milieu matériel parfaitement déformable. On regroupe sous cette...) (vision dite substantialiste) : le fluide calorique. Les corps étaient donc susceptibles de contenir une certaine quantité de ce fluide d'où l'appellation capacité calorifique. Pour des raisons historiques, la calorie était définie comme la « chaleur » nécessaire pour élever de 15 °C à 16 °C la température d'un gramme (Le gramme est une unité de masse du Système international (l'unité de base est le kilogramme) et...) d'eau (L’eau est un composé chimique ubiquitaire sur la Terre, essentiel pour tous les...), d'où le nom de capacité calorifique.

Aujourd'hui, on considère que l'énergie interne (En France, ce nom désigne un médecin, un pharmacien ou un chirurgien-dentiste, à la...) des systèmes est constituée des énergies cinétique (Le mot cinétique fait référence à la vitesse.) et potentielle microscopiques. La chaleur n'est plus un fluide, c'est un transfert d'énergie désordonnée à l'échelle microscopique. La capacité calorifique, est désormais appelée capacité thermique.

Capacité calorifique molaire à volume constant

On appelle capacité calorifique molaire à volume constant , le rapport de la quantité d'énergie transmise par chaleur nécessaire pour faire monter la température d'une mole de corps pur (En chimie, un corps pur est composé d'un seul type de constituant (contraire : mélange). Il...) d'une petite quantité par cette petite quantité soit :

en J/K/mol

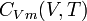
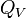
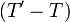
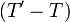
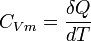
Il convient toujours de préciser que lors d'une petite variation d'un état à un autre état voisin , il y a un autre coefficient (En mathématiques un coefficient est un facteur multiplicatif qui dépend d'un certain...) très important, appelé coefficient calorifique de chaleur latente (L'enthalpie de changement d'état, molaire ou massique, correspond à la quantité de chaleur...) de dilatation :

, en Pascal (valant formule de Clapeyron):

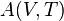
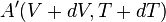
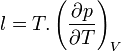
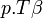
L'énergie thermique (L'énergie thermique est l'énergie cinétique d'un objet, qui est due à une agitation...) échangée au cours d'une transformation est donc :

où n'est qu'une forme différentielle et non pas la différentielle d'une fonction d'état. D'après le premier principe de la thermodynamique, δQ = dU − δW, où δW est le travail mis en jeu dans la transformation et U la fonction énergie interne. On retrouve donc sous une forme mathématique le fait qu'il n'existe pas de "chaleur" de la tasse à café chaude, malgré tout (Le tout compris comme ensemble de ce qui existe est souvent interprété comme le monde ou...) ce que peut véhiculer le langage ordinaire. Toutefois si seules les forces de pression (La pression est une notion physique fondamentale. On peut la voir comme une force rapportée...) sont susceptibles de travailler, δW = − p_e.dV, et on obtient dans le cas d'une transformation à volume constant δW = 0, d'où la définition (Une définition est un discours qui dit ce qu'est une chose ou ce que signifie un nom. D'où la...) plus précise de la capacité thermique isochore (La capacité thermique isochore, que l'on note le plus souvent , se définit par la dérivée...) d'un corps pur monophasé :

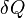
Capacités intensives

On peut déduire de la capacité thermique d'un corps de masse (Le terme masse est utilisé pour désigner deux grandeurs attachées à un...) m et de quantité de matière (La matière est la substance qui compose tout corps ayant une réalité tangible. Ses...) n, deux grandeurs associées intensives :

• La capacité thermique massique  : rapportée à un kilogramme (Le kilogramme (symbole kg) est l’unité de masse dans le Système international...) du corps considéré,
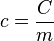
• La capacité thermique molaire  : rapportée à une mole du corps considéré.

Relation de Mayer

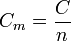
et sont liés entre eux et aux coefficients thermoélastiques par la relation de Mayer.

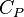
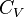
Capacité calorifique molaire à pression constante

C'est le même raisonnement mais en gardant cette fois la pression constante. Pratiquement, c'est aussi plus facile à mesurer.

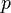
On introduit alors un coefficient de chaleur latente de compression  :

, avec , formule de Clapeyron (La formule de Clapeyron ou relation de Clausius-Clapeyron est une formule générale permettant de...)

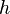
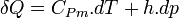
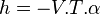
Plus précisément la capacité thermique isobare (La capacité thermique isobare que l'on note le plus souvent , se définit par la relation :) d'un corps pur monophasé est définie à partir de son enthalpie (L'enthalpie (du préfixe en- et du grec thalpein: chauffer) est une fonction d'état de la...) H = U + p.V :