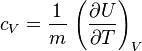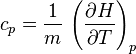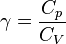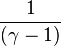Capacité thermique massique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La chaleur massique ou chaleur spécifique (symbole c ou s), qu'il convient d'appeler capacité thermique massique, est déterminée par la quantité d'énergie à apporter par échange thermique pour élever d'un Kelvin la température de l'unité de masse d'une substance. C'est donc une grandeur intensive égale à la capacité thermique rapportée à la masse du corps étudié.
L'unité du système international est alors le joule par kilogramme-kelvin (J·kg-1·K-1). La détermination des valeurs des capacités thermiques des substances relève de la calorimétrie.
Suivant le type de transformation thermodynamique, on considère soit l'énergie interne massique, soit l'enthalpie massique. Si on note U l'énergie interne, H l'enthalpie et m la masse d'un corps on a donc les capacités thermiques massiques :
La différence entre la chaleur spécifique à pression constante cp et la chaleur spécifique à volume constant cV est liée au travail qui doit être fourni pour dilater le corps en présence d'une pression externe. Si elle est souvent négligeable pour les phases condensées réputées peu compressibles et peu dilatables (liquides ou solides) la différence entre cV et cp est importante pour les gaz.
Cas des gaz parfaits
D'après la théorie cinétique des gaz, l'énergie interne d'une mole de gaz parfait monoatomique est égale à (3/2)RT, et plus élevée pour les gaz dont les molécules sont polyatomiques ; par exemple, (5/2)RT pour un gaz diatomique. Le calcul théorique n'est plus possible pour les molécules complexes.
La capacité massique à volume constant est ainsi de :
-
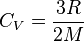
-
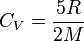
La capacité massique à pression constante d'un gaz parfait peut être déterminée à partir de la capacité massique à volume constant, puisque l'équation des gaz parfaits exprime que :
-
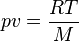
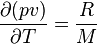
p étant la pression, v le volume massique, R la constante molaire des gaz, et M la masse molaire du gaz considéré.
La différence théorique entre ces deux valeurs est ainsi :
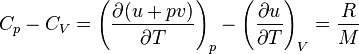
Le rapport des deux capacités d'un gaz est important en thermodynamique ; il est noté gamma :
Sa valeur dépend de la nature du gaz considéré ; pour un gaz parfait, la valeur théorique de γ est :
- γ = 5/3= 1,67 pour un gaz monoatomique (1/(γ-1)=3/2=1,5) ;
- γ = 7/5= 1,4 pour un gaz diatomique (1/(γ-1)=5/2=2,5).
| Gaz | Masse molaire (kg/mol) | température (°C) | Cv capacité massique J/(kg.K) |
|
|---|---|---|---|---|
| Air | 29×10-3 | 0-100 | 710 | 2,48 |
| Argon | 39,948×10-3 | 15 | 320 | 1,54 |
| Azote | 28,013×10-3 | 0-200 | 730 | 2,46 |
| Dioxyde de carbone | 44,01×10-3 | 20 | 650 | 3,44 |
| Hélium | 4,003×10-3 | 18 | 3160 | 1,52 |
| Hydrogène | 2,016×10-3 | 16 | 10140 | 2,46 |
| Oxygène | 31,999×10-3 | 13-207 | 650 | 2,50 |
| Vapeur d'eau | 18,015×10-3 | 100 | 1410 | 3,06 |
Mesure de la capacité thermique massique d'un solide
La capacité thermique massique d'un solide peut être mesurée en utilisant un appareil de type ATD (analyse thermodifférentielle, ou DSC pour differential scanning calorimetry). Elle peut se définir de la façon suivante : quand un système passe de la température T à une température T+dT, la variation d’énergie interne du système dU est liée à la quantité de chaleur échangée δQ selon :
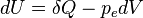
avec pe la pression extérieure à laquelle est soumis le système et dV la variation de volume. Si V=Cte:
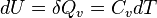
En revanche, si la transformation est isobare (pression constante), on obtient en utilisant la fonction enthalpie du système, la relation :
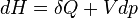
Si P= cte
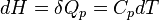
avec Cp la capacité à pression constante. La mesure consiste donc à mesurer la différence de température créée par un échange thermique donné, ou le flux d'énergie se traduit par une différence de température.
Le schéma suivant illustre la technique instrumentale utilisée dans le cas de la première méthode (mesure de la différence de température).
L’appareil est constitué de deux « plots » indépendants et d’un four. Des thermocouples permettent de mesurer la température de la face supérieure des plots en contact avec l’échantillon, ainsi que la température du four. Celle-ci correspond à la température de mesure. Toutes les mesures sont effectuées en utilisant un porte-échantillon d’aluminium vide sur l’un des plots. Une première mesure d’un autre porte-échantillon d’aluminium vide permet d’obtenir une ligne de base (dépendant de la mesure de température par les thermocouples). Puis une mesure d’un échantillon de référence de chaleur massique connue permet d’étalonner l’appareil. Enfin, l’échantillon sous forme de poudre est mesuré et sa chaleur massique est obtenue par comparaison avec celle de l’échantillon de référence. Pour améliorer la précisions de la mesure, il convient de prendre en compte le cas échéant la différence de masse entre les deux porte échantillons (la correction s'effectue en utilisant la chaleur massique de l'aluminium). La source d’erreur principale provient de la qualité du contact thermique entre le plot et le porte-échantillon.