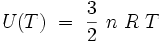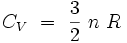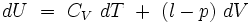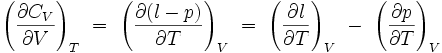Capacité thermique isochore - Définition
La capacité thermique isochore, que l'on note le plus souvent
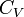
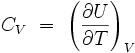
|
Comme l'énergie interne, c'est une grandeur extensive, qui s'exprime en Joule par Kelvin. Elle dépend en général de la température T et du volume V.
Exemple
Pour n moles d'un gaz parfait monoatomique, l'énergie interne se calcule explicitement :
|
|
où R est la constante des gaz parfaits. L'énergie interne est ici indépendante du volume V, et la capacité thermique isochore est dans ce cas particulier égale à une constante :
|
|
Propriété
L'énergie interne U(T,V) étant en général une fonction de la température T et du volume V, la capacité thermique isochore s'introduit naturellement dans la forme différentielle :
|
|
où l est un coefficient calorimétrique.
Variation avec le volume
L'énergie interne U étant une fonction d'état, la forme différentielle précédente est une différentielle exacte, et on en déduit la relation :
|
|
La thermodynamique permet de montrer par ailleurs que le coefficient calorimétrique l est égal à :
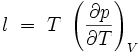
|
On en déduit la dérivée partielle de la capacité thermique isochore par rapport au volume à température constante :
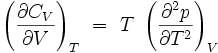
|
Si l'on connait l'équation d'état du système étudié, on peut donc calculer cette dérivée partielle.
Variation avec la température
La thermodynamique ne permet hélas pas de calculer la dérivée partielle de la capacité thermique isochore par rapport à la température à volume constant :
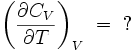
|
Cette variation doit donc être mesurée expérimentalement pour chaque système.