Cardinal inaccessible - Définition

Deux caractérisations de l'inaccessibilité à l'aide de la théorie des modèles

D'une part, un cardinal κ est inaccessible si et seulement si κ a la propriété réflexive (en) suivante : pour tous les sous-ensembles U ⊂ V_κ, il existe α < κ tel que est une sous-structure élémentaire (en) de (en fait, l'ensemble de ces α est fermé et non majoré (en) dans κ). Cela équivaut à dire que κ est -indescriptible (en) pour tous les n ≥ 0.

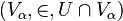
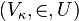
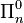
On peut démontrer dans ZF que ∞ satisfait une propriété réflexive un peu plus faible, pour laquelle la sous-structure (V_α, ∈, U ∩ V_α) n'est exigée "élémentaire" que par rapport à un sous-ensemble fini de formules. La raison ultime de cet affaiblissement est qu'alors que la relation de satisfiabilité (au sens de la théorie des modèles) peut être définie, la notion de vérité elle-même ne peut l'être, à cause du théorème de Tarski.

D'autre part, ZFC permet de montrer que κ est inaccessible si et seulement si (V_κ, ∈) est un modèle de ZFC au sens de la logique du second ordre (en). Alors, d'après la propriété de réflexivité précédente, il existe α < κ tel que (V_α, ∈) est un modèle standard de ZFC (considéré comme une théorie du premier ordre). Ainsi, l'existence d'un cardinal inaccessible est une hypothèse plus forte que celle de l'existence d'un modèle standard de ZFC.

Cardinaux α-inaccessibles ; cardinaux hyper-inaccessibles

Si α est un ordinal quelconque, un cardinal κ est dit α-inaccessible si et seulement si κ est inaccessible et si pour tout ordinal β < α, l'ensemble des cardinaux β-inaccessibles inférieurs à κ n'est pas majoré dans κ, et donc de cardinal κ, puisque κ est régulier.

Les cardinaux α-inaccessibles sont des points fixes des fonctions comptant les inaccessibles d'ordre inférieur. Par exemple, soit ψ₀(λ) le λ^ème cardinal inaccessible ; alors les points fixes de ψ₀ sont les cardinaux 1-inaccessibles. Par récurrence transfinie, soit ψ_β(λ) le λ^ème cardinal β-inaccessible, alors les points fixes de ψ_β sont les cardinaux (β+1)-inaccessibles (les valeurs de ψ_β+1(λ)) ; si α est un ordinal limite, un cardinal α-inaccessible est un point fixe de chaque ψ_β pour β < α (la valeur ψ_α(λ) étant le λ^ème cardinal ayant cette propriété).

On voit facilement que l'axiome des univers implique l'existence d'ordinaux α tels qu'il y ait α ordinaux inaccessibles plus petits (mais ils ne sont pas forcément inaccessibles eux-mêmes, et donc, d'après la définition, pas forcément 1-inaccessibles) ; en effet la fonction φ₀ donnant le plus petit ordinal α=φ₀(β) tel qu'il y ait β ordinaux inaccessibles < α est normale (en) (contrairement à ψ₀), et satisfait donc au théorème du point fixe (en) (pour les ordinaux). En revanche, l'existence d'un ordinal 1-inaccessible est strictement plus forte que l'axiome des univers, comme on l'a vu à la section précédente  : si α est le plus petit ordinal 1-inaccessible, V_α est un modèle de ZFCU ne contenant pas de cardinaux 1-inaccessibles. Plus généralement, le même argument montre que si α<β, l'axiome affirmant l'existence d'un cardinal β-inaccessible est strictement plus fort que l'axiome affirmant l'existence d'une classe propre d'ordinaux α-inaccessibles (voir à ce sujet la hiérarchie de cohérence relative des axiomes de grands cardinaux).

Un cardinal κ est dit hyper-inaccessible si et seulement si κ est κ-inaccessible (il ne peut bien sûr pas être κ+1-inaccessible). Comme précédemment, pour tout ordinal α, on dit qu'un cardinal κ est α-hyper-inaccessible si κ est hyper-inaccessible et si pour tout β < α, l'ensemble des β-hyper-inaccessibles inférieurs à κ n'est pas majoré dans κ. Généralisant ces constructions à la notion d'hyper-hyper-inaccessible (les cardinaux κ qui sont κ-hyper-inaccessibles), puis d'α-hyper-hyper-inaccessible, etc., on aboutit aux cardinaux Mahlo (en), lesquels sont les cardinaux κ qui sont hyper^κ-inaccessibles.