Cardinal inaccessible - Définition

Introduction

En mathématiques, et plus précisément en théorie des ensembles, un cardinal inaccessible est un cardinal ne pouvant être construit à partir de cardinaux plus petits à l'aide des axiomes de ZFC ; cette propriété fait qu'un cardinal inaccessible est un grand cardinal.

Définitions

Rappelons d'abord qu'un cardinal est dit limite s'il est de la forme , où α est un ordinal limite (sinon, on dit que est le successeur de ) ; d'autre part, on dit qu'un ordinal α est cofinal avec un ordinal β inférieur s'il existe une application strictement croissante f de β dans α tel que α soit la limite de f au sens suivant :  ; on dira alors qu'un cardinal est régulier s'il n'est cofinal avec aucun cardinal strictement plus petit, et qu'il est singulier dans le cas contraire. Tous les cardinaux successeurs sont réguliers ; est également régulier (mais, par exemple, est singulier, puisqu'il est la limite de la suite dénombrable des ). On dit alors enfin qu'un cardinal , non dénombrable, est faiblement inaccessible s'il est limite et régulier ; et qu'il est fortement inaccessible (ou simplement inaccessible) s'il vérifie de plus la condition . Si l'on admet l'hypothèse généralisée du continu, les deux notions se confondent. Une condition caractéristique pour être un ordinal faiblement inaccessible est d'être régulier et limite d'ordinaux réguliers.

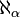
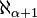
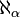
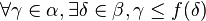
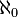
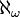
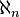
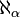
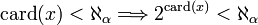
L'axiome des univers de Grothendieck

Beaucoup d'axiomes de grands cardinaux se généralisent sous la forme "il existe une classe propre de cardinaux ayant la propriété P", où P est une propriété de grand cardinal ; on voit aisément que cela équivaut à "Pour tout cardinal α il existe un cardinal β tel que α<β et P(β)". Dans le cas de l'inaccessibilité, l'axiome correspondant est donc "Pour tout cardinal μ, il existe un cardinal inaccessible κ tel que μ < κ" ; les arguments précédents montrent qu'il s'agit là d'un axiome beaucoup plus fort que la simple existence d'un seul cardinal inaccessible. En supposant ZFC, cet axiome est équivalent à l'axiome des univers de Grothendieck et Verdier : tout ensemble est contenu dans un univers de Grothendieck, c'est-à-dire dans un ensemble "stable" pour la réunion et l'ensemble des parties. La théorie formée des axiomes de ZFC et de l'axiome des univers est notée ZFCU ; ce système axiomatique est utile en particulier en théorie des catégories, où il permet de montrer, par exemple, que toute (petite) catégorie possède un plongement de Yoneda. Cet axiome reste cependant relativement faible (en tant qu'axiome de grand cardinal), puisque dans le langage de la section suivante, il revient à dire que ∞ est 1-inaccessible, où ∞ désigne le plus petit ordinal non dans V, c'est-à-dire la classe de tous les ordinaux du modèle V choisi.

Modèles et cohérence

Cardinaux fortement inaccessibles

On construit dans ZF la hiérarchie cumulative de von Neumann, V_α, α étant un ordinal, qui est une hiérarchie de tous les ensembles bien fondés, de tous les ensembles en présence de l'axiome de fondation. En particulier V_α contient tous les ordinaux strictement inférieurs à α.

On montre alors dans ZF que, si κ est (fortement) inaccessible — on dira juste inaccessible dans la suite — l'ensemble V_κ, muni de l'appartenance restreinte à V_κ est un modèle de ZF. On peut ajouter l'axiome du choix : dans ZFC, on montre que V_κ est un modèle de ZFC. On a besoin de la régularité de κ pour démontrer le schéma d'axiomes de remplacement.

On déduit de ce résultat que tout modèle U de ZFC (ou univers), ou bien ne contient pas de cardinaux inaccessibles, ou bien en contient et dans ce cas en contient un plus petit soit κ ; V_κ muni de l'appartenance de l'univers U restreinte à V_κ, soit ∈_Vκ, est alors un modèle de ZFC. De ce fait les cardinaux de (V_κ, ∈_Vκ), en tant que modèle de ZFC sont les cardinaux de U qui appartiennent à V_κ, c'est-à-dire les cardinaux de U strictement inférieur à κ. Il est par ailleurs facile de vérifier que les cardinaux inaccessibles dans (V_κ, ∈_Vκ) le seraient encore dans U, et donc (V_κ, ∈_Vκ) ne contient pas de cardinal inaccessible. D'où le résultat suivant.

Théorème. — Dans ZFC (avec axiome de fondation), supposée cohérente, on ne peut pas démontrer l'existence d'un cardinal inaccessible, c'est-à-dire que, si la théorie ZFC est cohérente, alors la théorie ZFC + « Il n'existe pas de cardinal inaccessible » est cohérente.

Cependant on a un résultat plus fort que la simple non démontrabilité de l'existence d'un cardinal inaccessible. En effet l'existence d'un cardinal inaccessible permet de démontrer l'existence d'un modèle de ZFC, c'est-à-dire la cohérence de cette théorie. Le second théorème d'incomplétude de Gödel permet d'en déduire le théorème précédent d'une façon plus détournée, mais également un résultat plus précis. Ainsi, dans la théorie ZFC + « il existe un cardinal inaccessible », on démontre des énoncés arithmétiques (comme la cohérence de la théorie ZFC exprimée en utilisant la démontrabilité) qui ne sont pas démontrables dans ZFC. A contrario, si on ajoute à ZFC l'hypothèse du continu, qui n'est pas non plus démontrable dans ZFC, on démontre les mêmes énoncés arithmétiques que dans ZFC.

On déduit également du second théorème d'incomplétude que la cohérence de la théorie ZFC + « il existe un cardinal inaccessible » n'est pas conséquence de la cohérence de la théorie ZFC, puisque sinon la théorie ZFC + « ZFC est cohérente » démontrerait sa propre cohérence. La théorie ZFC + « il existe un cardinal inaccessible » est en ce sens « plus forte » que la théorie ZFC.

Remarques :

• (V_κ, ∈_Vκ) peut être modèle de ZFC sans que l'ordinal κ soit un cardinal inaccessible, comme on le déduit des caractérisations de l'inaccessibilité en termes de modèles vues plus loin.
• si κ est un cardinal inaccessible d'un univers U, les classes de (V_κ, ∈_Vκ) sont, dans U, les parties de V_κ définissables par des formules avec paramètres dans V_κ et dont les quantificateurs sont restreints à V_κ. L'ensemble de ces parties est donc un modèle de la théorie des classes de Von-Neumann-Bernays-Gödel.
• Pour des raisons analogues V_κ+1 est un modèle de la théorie des classes de Morse-Kelley. La cohérence de cette théorie (et celle de la théorie précédente) se démontrent donc dans la théorie ZFC + « il existe un cardinal inaccessible ».

Cardinaux faiblement inaccessibles

On obtient essentiellement les mêmes résultats pour les cardinaux faiblement inaccessibles que pour les cardinaux inaccessibles : l'existence d'un cardinal faiblement inaccessible n'est pas démontrable et la cohérence de ZFC + « il n'existe pas de cardinal faiblement inaccessible » se déduit de la cohérence de ZFC, la non-existence d'un cardinal faiblement inaccessible n'est pas démontrable non plus (si ZFC est cohérente), car la cohérence de ZFC se démontre dans la théorie ZFC + « il existe de cardinal faiblement inaccessible ».

Cependant, si les démonstrations suivent la même ligne, elles reposent sur les propriétés beaucoup plus délicates à établir d'une autre construction, la hiérarchie des ensembles constructibles (L_α), définie inductivement pour tout ordinal α, et que Gödel a utilisé pour démontrer la cohérence de l'hypothèse du continu, mais aussi de l'hypothèse généralisée du continu (HGC dans la suite) et de l'axiome du choix, relativement à ZF.

La définition de la hiérarchie des L_α différe de celle des V_α pour α successeur : L_α+1 est l'ensemble des sous-ensembles définissables de L_α avec paramètres dans L_α. La réunion (au sens intuitif) des L_α est la classe L, qui, munie de la restriction de la relation d'appartenance à L, définit un modèle de ZFC + HGC dans tout univers de ZF. Dans un tel modèle, comme il satisfait HGC, un cardinal faiblement inaccessible est inaccessible. On vérifie que L conserve les mêmes ordinaux, et que les cardinaux faiblement inaccessibles de l'univers le sont encore pour le sous-univers défini par L. Si κ est un cardinal faiblement inaccessible, L_κ définit un modèle de ZFC(+HGC).

On en déduit alors les résultats d'indépendance annoncés en début de paragraphe de la même façon qu'au paragraphe précédent.