Axiome de fondation - Définition

L'axiome de fondation, encore appelé axiome de régularité, est l'un des axiomes de la théorie axiomatique des ensembles. Introduit en 1925 par John von Neumann, il joue un grand rôle dans cette théorie, alors que les mathématiciens ne l'utilisent jamais ailleurs, même s'ils le considèrent souvent intuitivement vérifié. L'axiome de fondation fait ou non partie des axiomes de ZF (et ZFC) suivant les ouvrages.

Définition

L'axiome de fondation stipule que

pour tout ensemble x non vide, il existe un ensemble y appartenant à x et n'ayant aucun élément en commun avec x,

en écriture symbolique

∀x[x ≠ ∅ ⇒ ∃y(y ∈ x et y ∩ x = ∅)]

Par exemple, si x a pour élément l'ensemble vide, ce dernier conviendra pour y. C'est même le seul choix possible si x est un ensemble transitif non vide (qui a donc forcément l'ensemble vide pour élément).

Dans un univers de la théorie des ensembles qui satisfait l'axiome de fondation, les ensembles décrits par la théorie axiomatique reflètent davantage l'image intuitive :

• aucun ensemble n'est élément de lui-même : on ne peut avoir , puisque sinon le singleton {x} fournirait un contre-exemple à l'axiome de fondation : {x} ∩ x = {x} ;
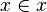
• plus généralement, la relation d'appartenance n'a pas de cycle : on ne peut avoir et ... et , puisque sinon {x₀, …, x_n} contredirait l'axiome de fondation ;
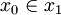
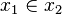
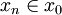
• plus généralement encore, on ne peut avoir de suite infinie d'ensembles tels que , , … , , …, puisque l'ensemble image de cette suite, {x_n | n ∈ N}, contredirait l'axiome de fondation.

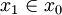
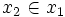
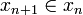
Cette dernière propriété signifie que le prédicat à deux variables libres "  " est bien fondé. Elle est équivalente à l'axiome de fondation si l'axiome du choix dépendant est vérifié. Ce dernier est un axiome du choix très faible qui permet de construire des suites et que le mathématicien, non spécialiste de logique mathématique, suppose intuitivement toujours vérifié, souvent sans le savoir.

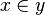
Axiome de fondation et paradoxe de Russell

En présence de l'axiome de fondation, on n'a jamais " x ∉ x ". Mais le rapport entre le paradoxe de Russell et l'axiome de fondation n'est qu'apparent. Ce dernier n'est en aucun cas une solution au paradoxe de Russell (apportée en théorie des ensembles par des restrictions au schéma d'axiomes de compréhension général). En effet le paradoxe de Russell utilise seulement la possibilité d'écrire " x ∉ x ". En présence de l'axiome de fondation la classe définie par x ∉ x est simplement l'univers de tous les ensembles, qui doit de toute façon être une classe propre. Les théories des ensembles ZFC avec axiome de fondation et ZFC avec la négation de l'axiome de fondation, sont équi-cohérentes (voir la suite).

La hiérarchie cumulative

La hiérarchie cumulative de von Neumann est définie par induction sur la classe de tous les ordinaux, en commençant par l'ensemble vide et en itérant l'ensemble des parties, c’est-à-dire que (P(E) désigne l'ensemble des parties de E) :

• V_α = ∪_β<α P(V_β)

et donc :

• V₀ = ∅
• V_α+1 = P(V_α)
• V_α = ∪_β<α V_β   pour tout ordinal limite α .

La classe (propre !) V est obtenue par réunion des V_α pour tous les ordinaux. Si " Ord " désigne la classe de tous les ordinaux :

V(x) ≡ ∃ α (Ord(α) et x ∈ V_α).

La classe V définit, à l'intérieur de tout modèle de la théorie des ensemble ZF ou ZFC, en gardant la même relation d'appartenance, un modèle de la théorie ZF (ZFC si l'univers initial est modèle de ZFC) qui satisfait AF, l'axiome de fondation. Ceci montre la cohérence relative de ZF+AF vis à vis de ZF, de même pour ZFC. Dit autrement, la négation de AF, l'axiome de fondation, n'est pas démontrable dans ZFC (et donc ZF).

On montre que, de plus, l'axiome de fondation est satisfait par un modèle de ZF si et seulement si ce modèle est réduit à la classe V. Dit autrement, l'axiome de fondation équivaut à la formule ∀x V(x). En présence de l'axiome de fondation, on peut donc définir le rang ordinal d'un ensemble a, qui est le plus petit ordinal α tel que a ∈ V_α.

Indépendance de l'axiome de fondation

L'axiome de fondation n'est pas démontrable à partir des axiomes de ZFC (bien sûr sans fondation). On montre, par une application très simple de la méthode de permutation de Fraenkel-Mostowski (on modifie la relation d'appartenance à l'aide d'une " permutation " sur l'univers de tous les ensembles), que si la théorie ZFC est cohérente, par exemple la théorie ZFC plus l'existence d'un ensemble a tel que a = {a} est cohérente.