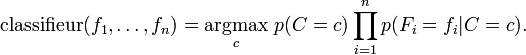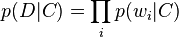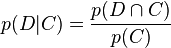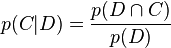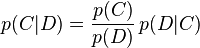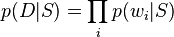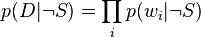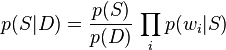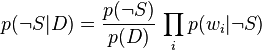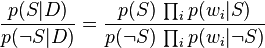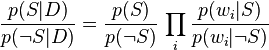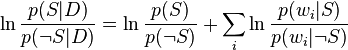Classification naïve bayesienne - Définition

Construire un classifieur à partir du modèle de probabilités

Jusqu'à présent nous avons établi le modèle à caractéristiques indépendantes, à savoir le modèle de probabilités bayésien naïf. Le classifieur bayésien naïf couple ce modèle avec une règle de décision. Une règle couramment employée consiste à choisir l'hypothèse la plus probable. Il s'agit de la règle du maximum a posteriori ou MAP. Le classifieur correspondant à cette règle est la fonction classifier suivante :

Estimation de la valeur des paramètres

Tous les paramètres du modèle (probabilités a priori des classes et lois de probabilités associées aux différentes caractéristiques) peuvent faire l'objet d'une approximation par rapport aux fréquences relatives des classes et caractéristiques dans l'ensemble des données d'entraînement. Il s'agit d'une estimation du maximum de vraisemblance des probabilités. Les probabilités a priori des classes peuvent par exemple être calculées en se basant sur l'hypothèse que les classes sont équiprobables (i.e chaque antérieure = 1 / (nombre de classes)), ou bien en estimant chaque probabilité de classe sur la base de l'ensemble des données d'entraînement (i.e antérieure de C = (nombre d'échantillons de C) / (nombre d'échantillons total)). Pour estimer les paramètres d'une loi de probabilité relative à une caractéristique précise, il est nécessaire de présupposer le type de la loi en question ; sinon, il faut générer des modèles non-paramétriques pour les caractéristiques appartenant à l'ensemble de données d'entraînement. Lorsque l'on travaille avec des caractéristiques qui sont des variables aléatoires continues, on suppose généralement que les lois de probabilités correspondantes sont des lois normales, dont on estimera l'espérance et la variance.

L'espérance, μ, se calcule avec

,

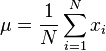
où N est le nombre d'échantillons et x_i est la valeur d'un échantillon donné.

La variance, σ², se calcule avec

.

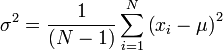
Si, pour une certaine classe, une certaine caractéristique ne prend jamais une valeur donnée dans l'ensemble de données d'entraînement, alors l'estimation de probabilité basée sur la fréquence aura pour valeur zéro. Cela pose un problème puisque l'on aboutit à l'apparition d'un facteur nul lorsque les probabilités sont multipliées. Par conséquent, on corrige les estimations de probabilités avec des probabilités fixées à l'avance.

Exemples

Classification des sexes

Problème: classifier chaque personne en temps qu'individu du sexe masculin ou féminin, selon les caractéristiques mesurées. Les caractéristiques comprennent la taille, le poids, et la pointure.

Entraînement

On dispose de l'ensemble de données d'entraînement suivant :

Sexe	Taille (cm)	Poids (kg)	Pointure (cm)
masculin	182	81.6	30
masculin	180	86.2	28
masculin	170	77.1	30
masculin	180	74.8	25
féminin	152	45.4	15
féminin	168	68.0	20
féminin	165	59.0	18
féminin	175	68.0	23

Le classifieur créé à partir de ces données d'entraînement, utilisant une hypothèse de distribution Gaussienne pour les lois de probabilités des caractéristiques, est le suivant :

Sexe	Espérance (taille)	Variance (taille)	Espérance (poids)	Variance (poids)	Espérance (pointure)	Variance (pointure)
masculin	178	2.9333e+01	79.92	2.5476e+01	28.25	5.5833e+00
féminin	165	9.2666e+01	60.1	1.1404e+02	18.25	2.1583e+01

On suppose pour des raisons pratiques que les classes sont équiprobables, à savoir P(masculin) = P(féminin) = 0.5 (selon le contexte, cette hypothèse peut être inappropriée). Si l'on détermine P(C) d'après la fréquence des échantillons par classe dans l'ensemble de données d'entraînement, on aboutit au même résultat.

Test

Nous voulons classifier l'échantillon suivant en tant que masculin ou féminin :

Sexe	Taille (cm)	Poids (kg)	Pointure (cm)
inconnu	183	59	20

Nous souhaitons déterminer quelle probabilité postérieure est la plus grande, celle que l'échantillon soit de sexe masculin, ou celle qu'il soit de sexe féminin.

postérieure (masculin) = P(masculin)*P(taille|masculin)*P(poids|masculin)*P(pointure|masculin) / évidence

postérieure (féminin) = P(féminin)*P(taille|féminin)*P(poids|féminin)*P(pointure|féminin) / évidence

Le terme évidence (également appelé constante de normalisation) peut être calculé car la somme des postérieures vaut 1.

évidence = P(masculin)*P(taille|masculin)*P(poids|masculin)*P(pointure|masculin) + P(féminin)*P(taille|féminin)*P(poids|féminin)*P(pointure|féminin)

Toutefois, on peut ignorer ce terme puisqu'il s'agit d'une constante positive (les lois normales sont toujours positives). Nous pouvons à présent déterminer le sexe de l'échantillon :

P(taille|masculin) = 1.5789 (La probabilité en un point peut être supérieure à 1 tant que l'aire sous la courbe Gaussienne vaut 1.)

P(poids|masculin) = 5.9881e-06

P(pointure|masculin) = 1.3112e-3

Postérieure (numérateur) (masculin) = 6.1984e-09

P(taille|féminin) = 2.2346e-1

P(poids|féminin) = 1.6789e-2

P(pointure|féminin) = 2.8669e-1

Postérieure (numérateur) (féminin) = 5.3778e-04

Comme la postérieure féminin est supérieure à la postérieure masculin, l'échantillon est donc de sexe féminin.

Classification et catégorisation de documents

Voici un exemple de classification bayésienne naïve appliquée au problème de la classification et catégorisation de documents. On souhaite ici classifier des documents par leur contenu, par exemple des E-mails en spam et non-spam. On imagine que les documents proviennent d'un certain nombre de classes de documents, lesquelles peuvent être définies comme des ensembles de mots dans lesquels la probabilité (indépendante) que le i-ième mot d'un document donné soit présent dans un document de la classe C peut s'écrire :

(Pour cette opération, nous simplifions l'hypothèse en supposant que les mots sont distribués au hasard dans le document, donc qu'ils ne dépendent ni de la longueur du document, ni de leur position respective à l'intérieur du document relativement à d'autres mots, ou autre contexte du document.)

On écrit donc la probabilité d'un document D, étant donné une classe C,

Quelle est la probabilité qu'un document D appartienne à une classe donnée C ? En d'autres termes, quelle est la valeur de ?

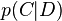
Par définition,

et

Le théorème de Bayes nous permet d'inférer la probabilité en termes de vraisemblance.

Si on suppose qu'il n'existe que deux classes mutuellement exclusives, S et ¬S (e.g. spam et non-spam), telles que chaque élément (email) appartienne soit à l'une, soit à l'autre,

et

En utilisant le résultat bayésien ci-dessus, on peut écrire :

En divisant les deux équations, on obtient :

Qui peut être factorisée de nouveau en :

Par conséquent, le rapport de probabilités p(S | D) / p(¬S | D) peut être exprimé comme une série de rapports de vraisemblance. La probabilité p(S | D) elle-même peut être inférée facilement avec log (p(S | D) / p(¬S | D)) puisqu'on observe que p(S | D) + p(¬S | D) = 1.

En utilisant les logarithmes de chacun de ces rapports, on obtient :

(Cette technique de rapport de vraisemblance est une technique courante en statistiques. Dans le cas de deux alternatives mutuellement exclusives (comme l'exemple ci-dessus), la conversion d'un rapport de vraisemblance en une probabilité prend la forme d'une sigmoïde. Voir logit pour plus de détails.)

Le document peut donc être classifié comme suit : Il s'agit de spam si (i.e. si ), sinon il s'agit de courrier normal.