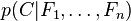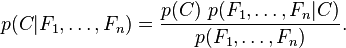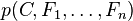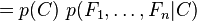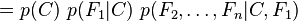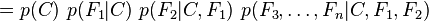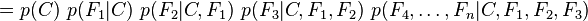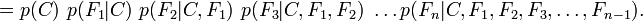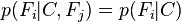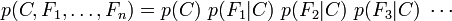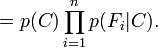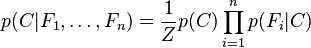Classification naïve bayesienne - Définition

Introduction

La classification naïve bayésienne est un type de classification Bayésienne probabiliste simple basée sur le théorème de Bayes avec une forte indépendance (dite naïve) des hypothèses. Elle met en oeuvre un classifieur bayésien naïf, ou classifieur naïf de Bayes, appartenant à la famille des classifieurs Linéaires.

Un terme plus approprié pour le modèle probabiliste sous-jacent pourrait être "modèle à caractéristiques statistiquement indépendantes".

En termes simples, un classifieur bayésien naïf suppose que l'existence d'une caractéristique pour une classe, est indépendante de l'existence d'autres caractéristiques. Un fruit peut être considéré comme une pomme s'il est rouge, arrondi, et fait une dizaine de centimètres. Même si ces caractéristiques sont liées dans la réalité, un classifieur bayésien naïf déterminera que le fruit est une pomme en considérant indépendamment ces caractéristiques de couleur, de forme et de taille.

Selon la nature de chaque modèle probabiliste, les classifieurs bayésiens naïfs peuvent être entraînés efficacement dans un contexte d'apprentissage supervisé. Dans beaucoup d'applications pratiques, l'estimation des paramètres pour les modèles bayésiens naïfs repose sur le maximum de vraisemblance. Autrement dit, il est possible de travailler avec le modèle bayésien naïf sans se préoccuper de probabilité bayésienne ou utiliser les méthodes bayésiennes.

Malgré leur modèle de conception "naïf" et ses hypothèses de base extrêmement simplistes, les classifieurs bayésiens naïfs ont fait preuve d'une efficacité plus que suffisante dans beaucoup de situations réelles complexes. En 2004, un article a montré qu'il existe des raisons théoriques derrière cette efficacité inattendue. Toutefois, une autre étude de 2006 montre que des approches plus récentes (arbres renforcés, forêts aléatoires) permettent d'obtenir de meilleurs résultats.

L'avantage du classifieur bayésien naïf est qu'il requiert relativement peu de données d'entraînement pour estimer les paramètres nécessaires à la classification, à savoir moyennes et variances des différentes variables. En effet, l'hypothèse d'indépendance des variables permet de se contenter de la variance de chacune d'entre elle pour chaque classe, sans avoir à calculer de matrice de covariance.

Le modèle bayésien naïf

Le modèle probabiliste pour un classifieur est le modèle conditionnel

où C est une variable de classe dépendante dont les instances ou classes sont peu nombreuses, conditionnée par plusieurs variables caractéristiques .

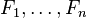
Lorsque le nombre de caractéristiques n est grand, ou lorsque ces caractéristiques peuvent prendre un grand nombre de valeurs, baser ce modèle sur des tableaux de probabilités devient impossible. Par conséquent, nous le dérivons pour qu'il soit plus facilement soluble.

A l'aide du théorème de Bayes, nous écrivons

En langage courant, cela signifie :

(voir les réseaux bayésiens)

En pratique, seul le numérateur nous intéresse, puisque le dénominateur ne dépend pas de C et les valeurs des caractéristiques F_i sont données. Le dénominateur est donc en réalité constant. Le numérateur est soumis à la loi de probabilité à plusieurs variables

et peut être factorisé de la façon suivante, en utilisant plusieurs fois la définition de la probabilité conditionnelle :

C'est là que nous faisons intervenir l'hypothèse naïve : si chaque F_i est indépendant des autres caractéristiques , alors

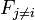
pour tout , par conséquent la probabilité conditionnelle peut s'écrire

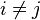
Par conséquent, en tenant compte de l'hypothèse indépendance ci-dessus, la probabilité conditionnelle de la variable de classe C peut être exprimée par

où Z (appelé "évidence") est un facteur d'échelle qui dépend uniquement de , à savoir une constante dans la mesure où les valeurs des variables caractéristiques sont connues.

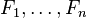
Les modèles probabilistes ainsi décrits sont plus faciles à manipuler, puisqu'ils peuvent être factorisés par l'antérieure p(C) (probabilité a priori de C) et les lois de probabilité indépendantes . S'il existe k classes pour C et si le modèle pour chaque fonction peut être exprimé selon r paramètres, alors le modèle bayésien naïf correspondant dépend de (k − 1) + n r k paramètres.

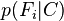
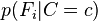
Dans la pratique, on observe souvent des modèles où k = 2 (classification binaire) et r = 1 (les caractéristiques sont alors des variables de Bernoulli). Dans ce cas, le nombre total de paramètres du modèle bayésien naïf ainsi décrit est de 2n + 1, avec n le nombre de caractéristiques binaires utilisées pour la classification.