Codage zeta - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le codage zeta ou codage de Boldi-Vigna est un codage entropique inventé par Paolo Boldi et Sebastiano Vigna en 2003 et utilisé essentiellement en compression de graphes.
Le code zeta produit est un code préfixe et universel.
Principe
Le codage zeta d'un entier naturel N dépend d'un paramètre k et se fait en deux étapes :
- le codage de l'exposant de la plus grande puissance de 2k inférieure ou égale à N avec un codage unaire ;
- le codage de la différence entre N et cette plus grande puissance avec un codage binaire tronqué.
Mathématiquement, pour coder un entier
![N, N \in \left [ (2^k)^h .. (2^k)^{h + 1} \right ]](https://static.techno-science.net/illustration/Definitions/autres/b/bd03db7b0902b2bda29129bb97b7ca87_a8a1efff00b9fec4a42d50748d6c7003.png)
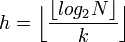
On appelle ζk la fonction associant à un entier naturel son code zeta paramétré par k.
Le codage zeta de paramètre 1 (utilisant la fonction ζ1) est équivalent au codage gamma et produit exactement les mêmes codes.
Codage des entiers relatifs
Comme pour les codages gamma, delta et omega, il est possible de coder des entiers relatifs avec le codage zeta en utilisant une bijection pour transformer les nombres négatifs ou nul en nombres strictement positifs avant le codage à proprement parler. Après le décodage, l'opération inverse doit être effectuée pour retrouver les entiers relatifs d'origine.
Exemples
| Décimal | Binaire | Code gamma | Code zeta k = 1 | Code zeta k = 2 | Code zeta k = 3 | Code zeta k = 4 |
|---|---|---|---|---|---|---|
| 1 | 00001 | 0 | 0 | 0 0 | 0 00 | 0 000 |
| 2 | 00010 | 10 0 | 10 0 | 0 10 | 0 010 | 0 0010 |
| 3 | 00011 | 10 1 | 10 1 | 0 11 | 0 011 | 0 0011 |
| 4 | 00100 | 110 00 | 110 00 | 10 000 | 0 100 | 0 0100 |
| 5 | 00101 | 110 01 | 110 01 | 10 001 | 0 101 | 0 0101 |
| 6 | 00110 | 110 10 | 110 10 | 10 010 | 0 110 | 0 0110 |
| 7 | 00111 | 110 11 | 110 11 | 10 011 | 0 111 | 0 0111 |
| 8 | 01000 | 1110 000 | 1110 000 | 10 1000 | 10 00000 | 0 1000 |

















































