Code de Lehmer - Définition
La liste des auteurs de cet article est disponible ici.
Décodage
Propriété — Le code de Lehmer L est une bijection de
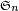
![\scriptstyle\ [\![1,1]\!]\times[\![1,2]\!]\times[\![1,3]\!]\times\dots\times[\![1,n]\!].](https://static.techno-science.net/illustration/Definitions/autres/d/d0b53aeac0e1ba26abd6599dcf14cd62_02356bc1a307593d7b4690131f4ec202.png)
Un algorithme
Un algorithme simple permet de reconstituer σ à partir de ƒ=L(σ). Par exemple, le code ƒ=113252 correspond à une permutation σ telle que σ(6)=2. En effet on voit que, par définition, L(σ,n)=σ(n). C'est le premier pas de l'algorithme :
- σ-1=x6xxxx ;
l'avant-dernier terme de la suite ƒ, égal à L(σ,5)=5, signifie que parmi les 5 images possibles pour 5, (1,3,4,5,6), il faut choisir la 5ème, σ(5)=6 :
- σ-1=x6xxx5 ;
le terme 2=L(σ,4), en 4ème position de la suite ƒ, signifie que parmi les 4 images possibles pour 4, (1,3,4,5), il faut choisir la 2ème, σ(4)=3 :
- σ-1=x64xx5 ;
le terme 3=L(σ,3), en 3ème position de la suite ƒ, signifie que parmi les 3 images possibles pour 3, (1,4,5), il faut choisir σ(3)=5 :
- σ-1=x64x35 ;
on termine avec σ(2)=1 :
- σ-1=264x35 ;
puis σ(1)=4 :
- σ-1=264135 ;
on a donc σ=(4,1,5,3,6,2). Il est clair d'après le déroulement de l'algorithme qu'à chaque pas il y a un choix pour σ(k), et il n'y en a qu'un. Donc chaque suite ƒ de
![\scriptstyle\ [\![1,1]\!]\times[\![1,2]\!]\times[\![1,3]\!]\times\dots\times[\![1,n]\!]\](https://static.techno-science.net/illustration/Definitions/autres/3/3fbfbf6b2a44115a00f3dc87323f99bd_62b24461209fe8eb8aadaa12b7fef9d5.png)
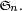
Un algorithme alternatif
Une autre possibilité est de construire σ-1 directement à partir de ƒ=113252 de la manière suivante :
- insérer 1 à la 1ère et seule place possible dans la suite x, ce qui donne 1,
- insérer 2 à la 1ère des places possibles dans la suite x1x, ce qui donne 21,
- insérer 3 à la 3ème des places possibles dans la suite x2x1x, ce qui donne 213,
- insérer 4 à la 2ème des places possibles dans la suite x2x1x3x, ce qui donne 2413,
- insérer 5 à la 5ème des places possibles dans la suite x2x4x1x3x, ce qui donne 24135,
- insérer 6 à la 2ème des places possibles dans la suite x2x4x1x3x5x, ce qui donne 264135.
On peut maintenant déduire σ de σ-1. Cette construction est justifiée par l'observation suivante : par définition, ƒ(i) est le rang de σ(i) quand on range la suite (σ(1), σ(2), σ(3), ... , σ(i-1), σ(i)) dans l'ordre croissant.
A voir
Notes
- (en) D.H. Lehmer, « Teaching combinatorial tricks to a computer », dans Proc. Sympos. Appl. Math. Combinatorial Analysis, Amer. Math. Soc., vol. 10, 1960, p. 179-193
- voir Charles-Ange Laisant, « Sur la numération factorielle, application aux permutations », dans Bulletin de la Société Mathématique de France, vol. 16, 1888, p. 176–183 , mais aussi (en) Don Knuth, The art of computer programming: Sorting and Searching, t. 3, Addison-Wesley, Reading, 1981, 2e éd., p. 12-13, où on fait référence à un article de Marshall Hall antérieur à celui de Lehmer. C'est probablement la raison pour laquelle Don Knuth parle d'"inversion table", et non pas de "Lehmer code".
- on utilise parfois une convention différente, avec des inégalités strictes plutôt que larges, en considérant le code
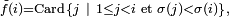
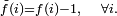
- Thomas S. Ferguson, « Who Solved the Secretary Problem? », dans Statistical Science, vol. 4, no 3, Août 1989, p. 282-289
Pages liées
- Permutation
- Nombre de Stirling
- Correspondance fondamentale de Foata
- Loi de Bernoulli
- The secretary problem
- Factoradic
Bibliographie
- (en) Roberto Mantaci et Fanja Rakotondrajao, « A permutation representation that knows what “Eulerian” means », dans Discrete Mathematics and Theoretical Computer Science, no 4, 2001, p. 101–108
- (en) Don Knuth, The art of computer programming: Sorting and Searching, t. 3, Addison-Wesley, Reading, 1981, 2e éd., p. 12-13

















































