Code de Lehmer - Définition
La liste des auteurs de cet article est disponible ici.
Définition
Le code de Lehmer, attribué à Derrick Lehmer, mais connu depuis 1888 au moins, associe à une permutation σ des éléments de
![\scriptstyle\ [\![1,n]\!]\](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/2f13ba6ef79e2c256c822e67f6e5a85f_eaf079bf872d4a443f973513a8981f8a.png)
Les applications ƒ, encodant des permutations de
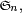
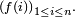
le code de Lehmer établit une correspondance L entre l'ensemble
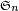
![[\![1,1]\!]\times[\![1,2]\!]\times[\![1,3]\!]\times\dots\times[\![1,n]\!].](https://static.techno-science.net/illustrationWebp/Definitions/autres/3/36732fadef15349ec240a2eeed1c8f1c_d4515fa4374848d2840dd3307efa8353.png)
Applications en combinatoire et en probabilités
Indépendance des rangs relatifs
Ces applications découlent d'une propriété immédiate du code de Lehmer L(σ) vu comme suite de nombres entiers.
Propriété — Sous la loi uniforme sur
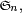
![\scriptstyle\ [\![1,i]\!]\](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/b88e6ac7abb5f88dc34c4560a736639a_236347cc22047c23ad8eb7ab1cb41695.png)
En d'autres termes, si on tire une permutation ω au hasard dans
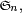
Nombre de records
Définition — Dans une suite u=(uk)1≤k≤n, il y a record vers le bas (resp. vers le haut) au rang k si uk est strictement plus petit (resp. strictement plus grand) que chaque terme ui tel que i
Soit B(k) (resp. H(k)) l'évènement "il y a record vers le bas (resp. vers le haut) au rang k" , i.e. B(k) est l'ensemble des permutations de
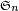
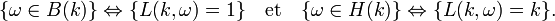
Ainsi le nombre Nb(ω) (esp. Nh(ω)) de records vers le bas (resp. vers le haut) de la permutation ω s'écrit comme une somme de variables de Bernoulli indépendantes de paramètres respectifs 1/k :
En effet, comme L(k) suit la loi uniforme sur
![\scriptstyle\ [\![1,k]\!],\](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a053d4521db1b9f4355f4114bc620fc6_eec718210e89bc0002e1e71d01a063da.png)
La fonction génératrice de la variable de Bernoulli
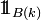
donc la fonction génératrice de Nb est
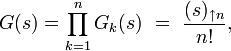
ce qui permet de retrouver la forme produit de la série génératrice des nombres de Stirling de première espèce (non signés).
Nombre de cycles
La correspondance fondamentale de Foata entraine que la loi de probabilité de Nb est aussi la loi du nombre de cycles de la décomposition d'une permutation tirée au hasard.
Problème des secrétaires
Il s'agit d'un problème d'arrêt optimal, classique en théorie de la décision, statistiques et probabilités appliquées, où une permutation aléatoire est dévoilée progressivement à travers les premiers termes de son code de Lehmer, et où il faut s'arrêter exactement à la valeur k telle que σ(k)=n, alors que la seule information disponible (les k premières valeurs du code de Lehmer) ne permet pas de calculer σ(k). En termes moins mathématiques, une série de n candidats sont présentés, l'un après l'autre, à un recruteur, qui doit recruter le meilleur, mais doit prendre sa décision ("je passe" ou "je recrute") au moment où le candidat lui est présenté, sans attendre d'avoir vu le candidat suivant (a fortiori, sans avoir vu tous les candidats). Le recruteur connait donc le rang du candidat présenté en k-ème position parmi les k candidats qu'il a déjà vu, donc, au moment de prendre sa k-ème décision ("je passe" ou "je recrute"), le recruteur connait les k premiers termes du code de Lehmer, alors qu'il aurait besoin de connaître la permutation : le recruteur aurait besoin de connaître tous les termes du code de Lehmer pour prendre une décision bien informée. Pour déterminer la stratégie optimale (optimisant la probabilité de gagner), les propriétés statistiques du code de Lehmer sont cruciales. Johannes Kepler aurait exposé clairement le problème des secrétaires à un ami au moment où il a entrepris de choisir sa seconde femme parmi 11 épouses potentielles (choix qu'il voulait faire très méticuleusement, son premier mariage, malheureux, ayant été arrangé sans qu'il ait été consulté).
