Nombre de Stirling - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, les nombres de Stirling apparaissent dans plusieurs problèmes combinatoires. Ils tirent leur nom de James Stirling, qui les a introduits au XVIIIe siècle. Il en existe deux sortes, nommés les nombres de Stirling de première espèce et les nombres de Stirling de seconde espèce.
Notations
Diverses notations sont utilisées pour les nombres de Stirling, mais celles que l'on rencontre le plus souvent sont
-
![\left[\begin{matrix} n \\ k \end{matrix}\right]](https://static.techno-science.net/illustration/Definitions/autres/e/e47262b105a6fff18f29b9bb79e0e7cd_ed72e4eef7b2e06f9aefbe9f9f76bedd.png)
-
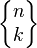
Cette notation, analogue à celle utilisée pour les coefficients binomiaux, est due à Jovan Karamata (en), qui l'a proposée en 1935, et dont l'usage a été encouragé par Donald Knuth ; on l'appelle la notation de Karamata.
Nombres de Stirling de seconde espèce
Les nombres de Stirling de seconde espèce
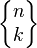
est le nème nombre de Bell. Si nous posons
(en particulier, (x)0 = 1 car il s'agit d'un produit vide) pour la factorielle décroissante, nous pouvons caractériser les nombres de Stirling de seconde espèce par
Table de valeurs
Voici quelques valeurs des nombres de Stirling de seconde espèce:
| n \ k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | |||||||||
| 1 | 0 | 1 | ||||||||
| 2 | 0 | 1 | 1 | |||||||
| 3 | 0 | 1 | 3 | 1 | ||||||
| 4 | 0 | 1 | 7 | 6 | 1 | |||||
| 5 | 0 | 1 | 15 | 25 | 10 | 1 | ||||
| 6 | 0 | 1 | 31 | 90 | 65 | 15 | 1 | |||
| 7 | 0 | 1 | 63 | 301 | 350 | 140 | 21 | 1 | ||
| 8 | 0 | 1 | 127 | 966 | 1701 | 1050 | 266 | 28 | 1 | |
| 9 | 0 | 1 | 255 | 3025 | 7770 | 6951 | 2646 | 462 | 36 | 1 |
Relation de récurrence
Ces nombres satisfont la relation de récurrence
avec
-
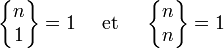
Identités simples
On a par exemple
et
Formule explicite
Les nombres de Stirling de seconde espèce sont donnés par la formule explicite
-
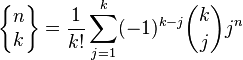
laquelle s'obtient en remarquant que le nombre de surjections (d'un ensemble de n éléments vers un ensemble de k éléments) peut se compter par la formule d'inclusion-exclusion : on compte toutes les applications moins celles n'atteignant pas un certain élément, plus celles n'atteignant pas deux éléments, moins...
Rapport avec la distribution de Poisson
Si X est une variable aléatoire suivant une distribution de Poisson avec une moyenne λ, alors son nème moment est
En particulier, le nème moment d'une distribution de Poisson de moyenne 1 est précisément le nombre de partitions d'un ensemble de taille n, qui est le nème nombre de Bell (formule de Dobinski).
Nombres de Stirling de première espèce
En combinatoire, les nombres de Stirling de première espèce non signés comptent le nombre de permutations de n éléments se décomposant en k cycles disjoints. De manière plus générale, ces nombres sont les valeurs absolues des nombres de Stirling de première espèce (signés), qui sont les coefficients du développement de
où (x)n est la factorielle décroissante
On peut inverser la définition afin d'exprimer xn comme une suite de factorielles croissantes :
Des relations similaires lient les nombres de Stirling de première espèce aux polynômes de Bernoulli. Un grand nombre de relations liées aux nombres de Stirling cachent des relations similaires liées aux coefficients binomiaux. L'étude des relations entre ces deux nombres est le calcul ombral et est un domaine important de la théorie des suites de Sheffer.
Table de valeurs
Voici une table donnant quelques valeurs des nombres de Stirling de première espèce, de la même forme que le triangle de Pascal:
| n \ k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | |||||||||
| 1 | 0 | 1 | ||||||||
| 2 | 0 | -1 | 1 | |||||||
| 3 | 0 | 2 | -3 | 1 | ||||||
| 4 | 0 | -6 | 11 | -6 | 1 | |||||
| 5 | 0 | 24 | -50 | 35 | -10 | 1 | ||||
| 6 | 0 | -120 | 274 | -225 | 85 | -15 | 1 | |||
| 7 | 0 | 720 | -1764 | 1624 | -735 | 175 | -21 | 1 | ||
| 8 | 0 | -5040 | 13068 | -13132 | 6769 | -1960 | 322 | -28 | 1 | |
| 9 | 0 | 40320 | -109584 | 118124 | -67284 | 22449 | -4536 | 546 | -36 | 1 |
Relation de récurrence
Les nombres de Stirling de première espèce satisfont la relation de récurrence
pour
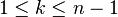
Ceci découle de la relation de récurrence des factorielles décroissantes :
-
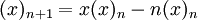
Identités simples
Remarquons que
et
et
Il en existe d'autres, comme
où Hn est un nombre harmonique et
où
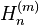
Formules explicites
On peut montrer la relation suivante entre nombres de Stirling de première et seconde espèce :
d'où, utilisant la formule explicite pour ces derniers qui sera donnée plus bas :
ou encore, après simplifications :
Fonction génératrice
Plusieurs identités peuvent être obtenues en manipulant la fonction génératrice
En particulier, l'ordre de la sommation peut être inversé; on peut également prendre des dérivées, ou encore fixer t ou x,
Sommes finies
Sommes infinies
qui est valide pour x < 1.
Interprétation énumérative
La valeur absolue du nombre de Stirling de première espèce compte le nombre de permutations de n objets ayant exactement k cycles. Par exemple,
![\left[\begin{matrix} 4 \\ 2 \end{matrix}\right]=11](https://static.techno-science.net/illustration/Definitions/autres/9/971917c5c896d6df12b45e250c7ca953_915ebf06b4dfcef0a5d24196ddb6880b.png)
- ( * * )( * * ) — 2 cycles de longueur 2
et huit permutations de la forme
- ( * * * ) — 1 cycle de longueur 3 et 1 cycle de longueur 1.
La valeur absolue du nombre de Stirling de première espèce compte aussi le nombre de permutations de n objets ayant exactement k records. Cette identité entre records et cycles résulte de la correspondance fondamentale de Foata. La de la série génératrice des nombres de Stirling de première espèce résulte de l'indépendance des termes du code de Lehmer d'une permutation, code très lié aux records d'une permutation.
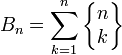
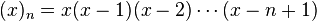
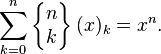
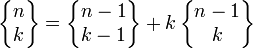
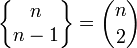
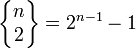
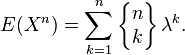
![(x)_n=\sum_{k=1}^n \left[\begin{matrix} n \\ k \end{matrix}\right]x^k](https://static.techno-science.net/illustration/Definitions/autres/2/2061a2a497fb51ce6ac68c239b94d394_c6a8ecb201dada3611c94245fea4b336.png)
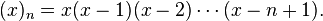
![x^n = \sum_{k=0}^n \left[\begin{matrix} n \\ k \end{matrix}\right] (x)^k](https://static.techno-science.net/illustration/Definitions/autres/d/d9e618deb9733fa45b5b0244d452e207_c2d2888fe4f879b2e6ac62bc31871e9d.png)
![\left[\begin{matrix} n+1 \\ k \end{matrix}\right] = \left[\begin{matrix} n \\ k-1 \end{matrix}\right] -n \left[\begin{matrix} n \\ k \end{matrix}\right]](https://static.techno-science.net/illustration/Definitions/autres/5/5b6152349716fb1a0e29d59bc48ce60a_aeefbd4744980643e17dcad012dd25af.png)
![\left[\begin{matrix} n \\ 0 \end{matrix}\right]=0 \quad \mbox { et } \quad \left[\begin{matrix} 1 \\ 1 \end{matrix}\right] = 1](https://static.techno-science.net/illustration/Definitions/autres/9/96ba908230d780a1844be40403751dd8_cac6999faa13a7226181ba912850a5a0.png)
![\left[\begin{matrix} n \\ 1 \end{matrix}\right] = (-1)^{n-1} (n-1)!](https://static.techno-science.net/illustration/Definitions/autres/a/a52e1adde1e26cc3dd14bd6515e17da2_5602eba64c43ebb5b379979b1e02fa7f.png)
![\left[\begin{matrix} n \\ n \end{matrix}\right] = 1](https://static.techno-science.net/illustration/Definitions/autres/3/33e76b5d4dca501a4e8b769d88dcd128_9208b134080f3eb35dd43bbcadba0db5.png)
![\left[\begin{matrix} n \\ n-1 \end{matrix}\right] = (-1)^n {n \choose 2}](https://static.techno-science.net/illustration/Definitions/autres/6/67868b1bb33c6ffa7b1492439dbab76f_749ce39c88ebb5e43581a50e1b19c2aa.png)
![\left[\begin{matrix} n \\ 2 \end{matrix}\right] = (-1)^n (n-1)!\; H_{n-1}](https://static.techno-science.net/illustration/Definitions/autres/5/556818794d559753ffe92779cef837ba_c7dd067a61f290a709068fcc4f90af24.png)
![\left[\begin{matrix} n \\ 3 \end{matrix}\right] = \frac {1}{2} (-1)^{n-1} (n-1)! \left[ (H_{n-1})^2 - H_{n-1}^{(2)} \right]](https://static.techno-science.net/illustration/Definitions/autres/d/d1cce48978d25e08dc34304e8952f975_574182f0acd75d2e225d7304cc912415.png)
![\left[\begin{matrix} n \\ m \end{matrix} \right]=\sum_{k=0}^{n-m}(-1)^k\binom{n-1+k}{n-m+k}\binom{2n-m}{n-m-k}\left\{\begin{matrix} n-m+k \\ k \end{matrix} \right\},](https://static.techno-science.net/illustration/Definitions/autres/8/88c10ce57ffe6fd25f2f88540da57b4d_2b08ee426992bd36431a8865f419870d.png)
![\left[\begin{matrix} n \\ m \end{matrix} \right]=\sum_{k=0}^{n-m}\sum_{j=0}^{k}\frac{(-1)^{2k-j}}{k!}\binom{n-1+k}{n-m+k}\binom{2n-m}{n-m-k}{k \choose j} j^{n-m+k},](https://static.techno-science.net/illustration/Definitions/autres/e/e59ec0f44b5283e31e4b4365f16006cb_5d6003c08f1ca437c39563d999c0ac85.png)
![\left[\begin{matrix} n \\ m \end{matrix} \right]=\frac{(2n-m)!}{(m-1)!}\sum_{k=0}^{n-m}\frac{1}{(n+k)(n-m-k)!(n-m+k)!}\sum_{j=0}^{k}\frac{(-1)^{j} j^{n-m+k} }{j!(k-j)!}.](https://static.techno-science.net/illustration/Definitions/autres/6/6a8c4917a53cca96db83c7818df7a005_ae585849817115fec4f38b94dc7753f1.png)
![(1+t)^x = \sum_{n=0}^\infty {x \choose n} t^n = \sum_{n=0}^\infty \frac {t^n}{n!} \sum_{k=0}^n \left[\begin{matrix} n \\ k \end{matrix}\right] x^k = \sum_{k=0}^\infty x^k \sum_{n=k}^\infty \frac {t^n}{n!} \left[\begin{matrix} n \\ k \end{matrix}\right] = e^{x\ln(1+t)}](https://static.techno-science.net/illustration/Definitions/autres/4/4ddf4929f54f141c7f51d92b922a49f2_326ddc0a977862b5bc75e0e938ba50b1.png)
![\sum_{k=0}^n (-1)^k \left[\begin{matrix} n \\ k \end{matrix}\right] = (-1)^n n!](https://static.techno-science.net/illustration/Definitions/autres/8/8f57420b15242c5b70368ebef35699d8_2039689d965e6fb6cbf0304bdf256e79.png)
![\sum_{n=m}^\infty \left[\begin{matrix} n \\ k \end{matrix}\right] \frac{x^n}{n!} = \frac {\left(\ln (1+x)\right)^m}{k!}](https://static.techno-science.net/illustration/Definitions/autres/2/2581639e38e02a8479d11f04d2b88d95_3196a7a1666665a8c6ae1fe955976eda.png)

















































