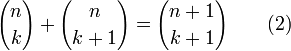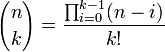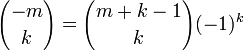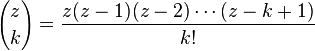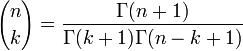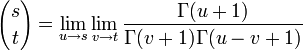Coefficient binomial - Définition
La liste des auteurs de cet article est disponible ici.
Définition algébrique des coefficients binomiaux d'entiers
Le coefficient binomial des entiers naturels n et k est noté
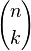
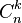
Ici n ! désigne la factorielle de n. On remarque qu'il existe deux notations : le coefficient binomial de n et k s'écrit
-
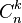
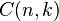
- ou bien
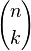
Une importante relation, la formule de Pascal, lie les coefficients binomiaux :
Elle donne lieu au triangle de Pascal qui permet un calcul rapide des coefficients pour de petites valeurs de n :
ligne 0: 1 ligne 1: 1 1 ligne 2: 1 2 1 ligne 3: 1 3 3 1 ligne 4: 1 4 6 4 1 ligne 5: 1 5 10 10 5 1 ligne 6: 1 6 15 20 15 6 1 ligne 7: 1 7 21 35 35 21 7 1 Les coefficients
![{n \choose k}, k \in [\![0;n]\!]](https://static.techno-science.net/illustration/Definitions/autres/6/6b6fa634462895b18a40e13cc32c5e49_7a012d7b1e074ebd3c094f981368d3a7.png)
Note : pour
![k \in [\![0;n]\!]](https://static.techno-science.net/illustration/Definitions/autres/b/bd87c214fbdff923c48a39b23da46abc_627b6b2f92e4a03707e19002d2856d2c.png)
La preuve de cette propriété se fait par récurrence :
- Pour
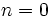
- Supposons que c'est vrai pour

- Regardons ce qui se passe lorsque
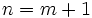
- pour
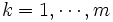
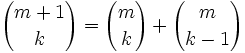
on y voit que
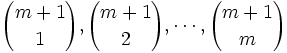
alors que
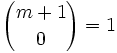
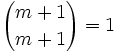
- La propriété est donc vraie pour
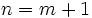
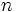
Généralisations
L'écriture de
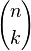
permet d'envisager une extension possible aussi pour tout entier n négatif et tout entier k strictement positif en utilisant l'expression suivante :
Si l'on pose n=-m, on a la relation suivante :
C'est cette forme des coefficients binomiaux qui est utilisée dans la formule du binôme négatif ainsi que dans la définition de la loi binomiale négative
Pour tout nombre complexe z et tout entier naturel k, on définit le coefficient binomial
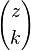
C'est cette forme des coefficients binomiaux qui est utilisée dans la formule du binôme généralisée.
Pour tout entier k, l'expression
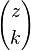
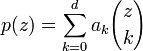
Une autre généralisation importante des coefficients binomiaux part de la formule du multinôme, laquelle permet de définir les coefficients multinomiaux.
Enfin, le calcul de
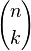
Comme la fonctionΓ est définie pour tout complexe de
-
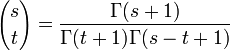
Cette formule peut d'ailleurs s'écrire plus simplement à l'aide de la fonction bêta :
-
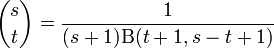
On peut tenter d'unifier les définitions avec la fonction Gamma, en résolvant le problème de pôles de cette fonction par un passage à la limite :
Mais il faut prendre garde à l'ordre des limites qui ne peuvent commuter et cette définition conduit à une valeur infinie du coefficient binomial dans les cas non étudiés précédemment
![\frac{n (n -1)(n - 2)\cdots (n - k +1)}{k!} = \begin{cases}\displaystyle \frac{n!}{k!(n-k)!} & \mbox{si } k \in [\![0;n]\!] \quad\mbox{(1)} \\\qquad 0 & \mbox{sinon}\end{cases}](https://static.techno-science.net/illustration/Definitions/autres/2/2bedb307f01abef61af756bd866e4b1c_04c7b1c1a49a75badd18ccf3bfdd894a.png)