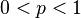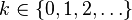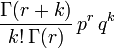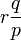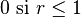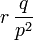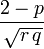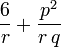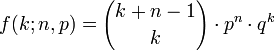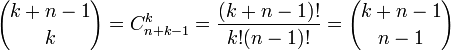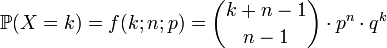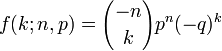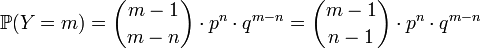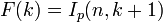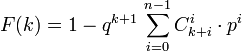Loi binomiale négative - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Binomiale négative | |
|---|---|
| |
| | |
| Paramètres |  (réel) (réel) |
| Support |
|
| Densité de probabilité (fonction de masse) |
|
| Fonction de répartition | Ip(r,k + 1) où Ip(x,y) est la fonction bêta incomplète régularisée |
| Espérance |
|
| Mode |  |
| Variance |
|
| Asymétrie (statistique) |
|
| Kurtosis (non-normalisé) |
|
| Fonction génératrice des moments |
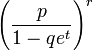
|
| Fonction caractéristique |
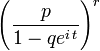
|
| modifier | |
En Probabilité et en Statistiques, la loi binomiale négative est une distribution de probabilité discrète. Elle décrit la situation suivante: une expérience consiste en une série de tirages indépendants, donnant un "succès" avec probabilité p (constante durant toute l'expérience) et un "échec" avec une probabilité complémentaire. Cette expérience se poursuit jusqu'à l'obtention d'un nombre donné n de succès. La variable aléatoire représentant le nombre d'échecs (avant l'obtention du nombre donné n de succès) suit alors une loi binomiale négative. Ses paramètres sont n, le nombre de succès attendus, et p, la probabilité d'un succès. Cette loi est aussi connue sous le nom de loi de Pascal en l'honneur de Blaise Pascal et de loi de Polya, en l'honneur de George Pólya.
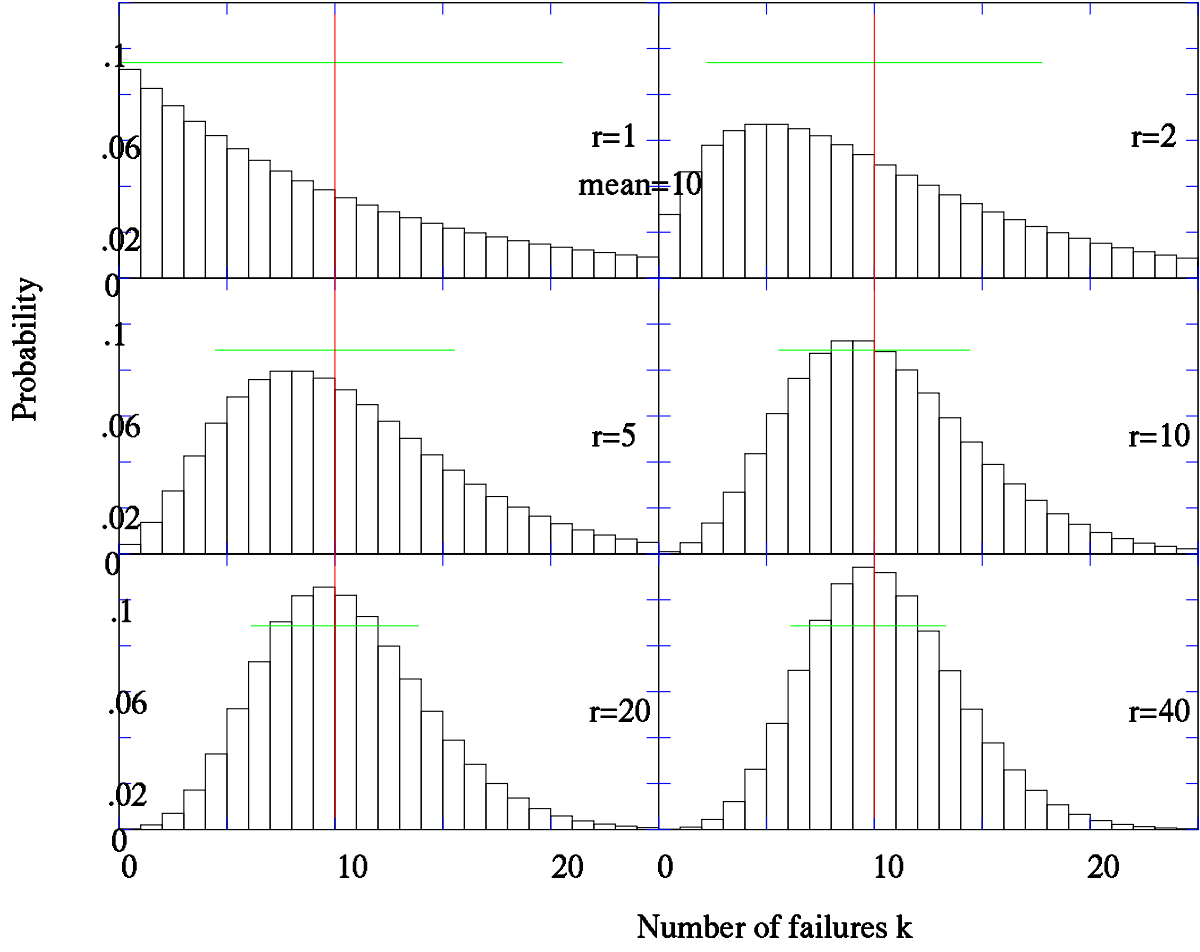
La loi se généralise à deux paramètres r et p, où r peut prendre des valeurs réelles strictement positives.
Loi binomiale négative à premier paramètre entier
Loi de probabilité
La loi binomiale négative dépend de deux paramètres, et plusieurs paramétrisations sont envisageables. Une paramétrisation très répandue introduit un entier naturel n non nul et un réel p compris entre 0 et 1. Il est courant d'introduire la probabilité complémentaire q = 1 − p. La loi de probabilité d'une variable aléatoire distribuée selon une binomiale négative de paramètres n et p, notée NegBin(n, p), prend la forme suivante : pour k = 0, 1, 2, ...
Le coefficient binomial est:
La loi binomiale négative est la loi de probabilité de la variable aléatoire X qui comptabilise le nombre d'échecs nécessaires avant obtention de n succès, sachant que la probabilité d'un succès est p :
La loi binomiale négative peut aussi s'écrire sous la forme
où
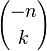
-
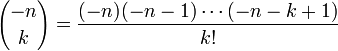
Cette expression justifie le nom de loi binomiale négative donnée à cette loi de probabilité. Elle facilite aussi, grâce à l'usage de la formule du binôme négatif, le calcul de son espérance
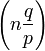
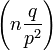
Définition alternative
On trouve parfois la définition alternative suivante: la loi binomiale négative de paramètres n et p est la loi de la variable aléatoire Y donnant le nombre d'essais nécessaires pour obtenir n succès. Alors pour tout
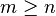
Les deux formules se déduisent l'une de l'autre. Il suffit de remarquer que Y = X + n et que m = k+n.
Dans la suite, on prendra la première définition pour définir de la loi binomiale négative.
Fonction de répartition
La fonction de répartition peut s'exprimer à l'aide de la fonction bêta incomplète régularisée:
Une démonstration par récurrence sur k prouve que