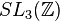Conjecture de Baum-Connes - Définition

Résultats partiels

La conjecture sans coefficients pour tous les groupes est toujours non résolue, bien que cette question ait été beaucoup étudiée. Elle a été démontrée pour les classes suivantes de groupes :

• les sous-groupes discrets de SO₀(n,1) et SU(n,1) ;
• les groupes ayant la propriété de Haagerup (en), ou groupes a-T-moyennables de Gromov ; ce sont les groupes agissant par isométries sur un espace de Hilbert affine de façon propre, au sens où pour tout et toute suite (g_n) d'éléments du groupe telle que . Parmi les groupes a-T-moyennables figurent les groupes moyennables (en), les groupes de Coxeter, les groupes agissant proprement sur un arbre ou sur un complexe cubique CAT(0) (en) simplement connexe ;
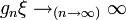
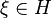
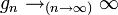
• les groupes qui admettent une présentation avec un nombre fini de générateurs et une seule relation ;
• les sous-groupes discrets cocompacts d'un groupe de Lie réel de rang 1 ;
• les réseaux cocompacts dans SL(3,K) avec K= . Le problème est resté longtemps ouvert, depuis les premiers jours de la conjecture, d'exhiber un groupe infini ayant la propriété T de Kazhdan (en) qui vérifie la conjecture. Mais Vincent Lafforgue en a trouvé un en 1998 et il a montré que les réseaux cocompacts dans SL(3, ) sont à décroissance rapide, donc vérifient la conjecture ;
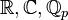
• les groupes hyperboliques (en) de Gromov et leurs sous-groupes.
• Parmi les groupes non discrets, la conjecture a été prouvée en 2003 par J. Chabert, S. Echterhoff et R. Nest pour la classe des groupes presque connexes (i. e. les groupes ayant une composante connexe cocompacte), et tous les groupes de points rationnels d'un groupe algébrique linéaire sur un corps local de caractéristique nulle (par exemple k= ). Pour la sous-classe des groupes réels réductifs, ceci avait déjà été prouvé en 1982 par A. Wassermann.

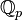
L'injectivité est connue pour bien plus de groupes grâce à la méthode Dirac-dual Dirac. Celle-ci remonte à des idées de Michael Atiyah, généralisées et formalisées en 1987 par Gennadi Kasparov. L'injectivité est connue pour les classes suivantes :

• les sous-groupes discrets de groupes de Lie connexes ou virtuellement connexes,
• les sous-groupes discrets des groupes p-adiques,
• les groupes boliques (qui sont une généralisation des groupes hyperboliques),
• les groupes agissant de façon moyennable sur un espace compact.

L'exemple le plus simple d’un groupe dont on ne sait pas s'il vérifie la conjecture est .