Conjecture de Baum-Connes - Définition

Introduction

En mathématiques, plus précisément en K-théorie des opérateurs (en), la conjecture de Baum-Connes suggère un lien entre la K-théorie de la C*-algèbre d'un groupe et la K-homologie (en) de l'espace classifiant les actions propres (en) de ce groupe.

Elle propose ainsi une correspondance entre deux objets mathématiques de nature différente, la K-homologie étant liée à la géométrie, à la théorie des opérateurs différentiels et à la théorie de l'homotopie, tandis que la K-théorie de la C*-algèbre réduite d'un groupe (en) est un objet purement analytique.

La conjecture, si elle était vraie, aurait pour conséquences quelques célèbres conjectures antérieures. Par exemple, la partie surjectivité implique la conjecture de Kadison-Kaplansky (en) pour un groupe discret sans torsion et la partie injectivité est étroitement liée à la conjecture de Novikov (en).

La conjecture est aussi très liée à la théorie de l'indice (en) (car l'application d'assemblage µ est une sorte d'indice) et joue un rôle majeur dans le programme de géométrie non commutative d'Alain Connes.

Les origines de la conjecture remontent à la théorie de Fredholm (en), au théorème de l'indice d'Atiyah-Singer (en), et à l'interaction entre la géométrie et la K-théorie des opérateurs telle qu'elle est formulée dans les travaux de Brown, Douglas et Fillmore, parmi bien d'autres sujets motivants.

Formulation

Soit Γ un groupe localement compact à base dénombrable (par exemple un groupe discret dénombrable). On peut définir le morphisme d'assemblage :

où et (k valant 0 ou 1) désignent respectivement :

• la K-homologie équivariante à supports Γ-compacts de l'espace qui classifie les actions propres de Γ,
• la K-théorie de la C*-algèbre réduite de Γ.

Paul Baum et Alain Connes ont conjecturé, en 1982, que

le morphisme d'assemblage μ est un isomorphisme.

Comme le membre de gauche semble moins difficile à calculer que celui de droite (parce qu'on connait très peu de théorèmes généraux de structure sur les C*-algèbres), on considère souvent cette conjecture comme une explicitation du membre de droite.

À l'origine, la conjecture n'était pas formulée en ces termes car la notion de K-homologie équivariante n'avait pas encore émergé.

Dans le cas où Γ est discret et sans torsion, le membre de gauche se réduit à la K-homologie non équivariante à supports compacts de l'espace classifiant (en) usuel BΓ de Γ.

Exemples

Soit Γ le groupe des entiers relatifs. Alors le membre de gauche est la K-homologie de son classifiant qui est le cercle. Par l'isomorphisme de Gelfand (en), qui n'est autre ici que la transformation de Fourier, la C*-algèbre du groupe est isomorphe à l'algèbre des fonctions continues sur le cercle, donc le membre de droite est la K-théorie topologique du cercle. Le morphisme d'assemblage est alors la dualité de Poincaré (en) en KK-théorie (définie par Gennadi Kasparov) et c'est un isomorphisme.

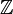
Un autre exemple simple est donné par les groupes compacts. Dans ce cas, les deux membres sont naturellement isomorphes à l'anneau des représentations complexes (en) du groupe K, et le morphisme d'assemblage, via ces isomorphismes, est l'application identité.

Conjecture à coefficients

Il existe aussi une forme plus générale, dite à coefficients, de la conjecture Baum-Connes, dans laquelle les deux membres sont à coefficients dans une C*-algèbre A sur laquelle Γ agit par automorphismes. Elle s'énonce dans le langage de la KK-théorie (en) en disant que le morphisme d'assemblage

est un isomorphisme, et la version sans coefficients correspond au cas .

Cependant, en 2002, Nigel Higson, Vincent Lafforgue et Georges Skandalis ont trouvé des contre-exemples à la conjecture à coefficients, en s'appuyant sur des résultats de Gromov (néanmoins non reconnus, en 2008, par la totalité de la communauté mathématique) qui concernent les expanseurs dans les graphes de Cayley. Même si cette construction se confirme, la conjecture à coefficients reste un sujet de recherche active car, contrairement à la conjecture classique, on la considère souvent comme un énoncé concernant des groupes ou ensembles de groupes particuliers.