Corps de rupture - Définition

Autres définitions

On rencontre cependant d'autres définitions du corps de rupture.

Certains appellent corps de rupture, tout corps dans lequel le polynôme P(X) possède une racine. C'est le cas par exemple de mathématiques.net. Selon cette acception serait un corps de rupture du polynôme

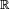
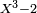
D'autres appellent corps de rupture d'un polynôme non constant tout corps de degré fini sur K dans lequel P soit scindé. C'est le cas de Lucien Chambadal. On trouve une définition proche de celle-ci dans l'article de l'Encyclopædia Universalis où le corps de rupture d'un polynôme P(X) est le corps engendré par K et l'ensemble des racines de P, c'est une définition proche de celle-ci que l'on rencontre chez François Le Lionnais.

Chez d'autres auteurs enfin, la recherche d'une extension minimale de K contenant une racine de P(X) reste une étape obligée pour la construction d'un corps de décomposition mais celle-ci n'a pas de nom spécifique. C'est le cas, par exemple, chez Bourbaki, chez Langou chez MacLane et Birkhoff.

Propriétés

Considérons l'anneau L défini par K[X] / (P) le quotient de l'anneau des polynômes à coefficients dans K par l'idéal engendré par P(X). L'application de K dans L qui associe à tout élément de K son polynôme (c'est un polynôme constant) est bien un morphisme.

• Montrons que L est un espace vectoriel sur K de dimension égale au degré de P(X).

La famille (1, α, α², α^n-1) où α est défini comme la classe de X est en effet une base de L. Cette famille est libre, car toute combinaison linéaire non nulle possède un représentant de degré strictement plus petit que n. Ce représentant ne peut être un multiple de P(X) et donc la combinaison linéaire n'est pas nulle. Soit alors A(X) un représentant d'un élément de L, la division euclidienne par P(X) montre qu'il existe un autre représentant R(X) de la classe de A(X) engendré par la famille. La classe de P(X) apparaît comme une combinaison linéaire de la base, égale à R(α), et la famille est génératrice. C'est donc bien une base et [L:K] est égal au degré du polynôme P(X).

• Montrons que L est un corps.

Comme il est déjà établi que L est un anneau, il suffit de démontrer que chaque élément différent de 0 est inversible. Soit l un élément non nul de L et R(X) un représentant dans K[X] de degré strictement inférieur à n. les deux polynômes R(X) et P(X) sont premiers entre eux car le dernier polynôme est irréductible et le premier de degré strictement inférieur à celui de P(X). L'identité de Bezout nous assure alors de l'existence de deux polynômes A(X) et B(X) tel que:

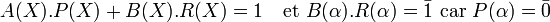
• Montrons que L possède une racine de P

Si α est défini comme la classe de X, P(α) est alors la classe de P(X). Mais la classe de P(X) est aussi la classe de 0. Donc P(α) = 0 et α est une racine de P.

• Montrons que tout corps de rupture de P(X) est isomorphe à K[X]/(P(X)).

Soit L' un corps de rupture de P(X). On définit un homomorphisme de K-algèbres de K[X] dans L' en envoyant X sur une racine de P(X) dans L'. L'idéal engendré par P(X) est dans le noyau de l'homomorphisme, on obtient donc par le théorème de factorisation un homomorphisme de K-algèbres de K[X] / (P(X)) dans L'. C'est injectif car K[X] / (P(X)) est un corps. Son l'image est une sous-extension de L' contenant une racine de P(x). Par sa minimalité, L' est donc égal à cette image. Le morphisme injectif est donc aussi surjectif, et L' est donc isomorphe à K[X] / (P(X)).

 

Par conséquent tout corps engendré par K et une racine de P(X) est un corps de rupture de P(X) de degré n sur K, isomorphe à K[X]/(P(X))

L'irréductibilité du polynôme P est nécessaire pour prouver l'unicité d'une extension minimale contenant une racine du polynôme. Un produit de deux polynômes irréductibles de degrés différents sur K aura deux extension de degré différents sur K, d'après ce qui précède, et donc non isomorphes. Même si les degrés sont les mêmes, les corps ne sont pas forcément isomorphes. Par exemple dans Q[X] (ici Q désigne le corps des nombres rationnels), le polynôme X⁴ - X² - 2 = (X²+1)(X²-2) possède deux extensions de corps de dimension minimale contenant une racine de P : Q[i] et Q[√2] Ces deux extensions ne sont pas isomorphes.

La clôture algébrique d'un corps est un sur-corps de K tel que tous les polynômes à coefficients dans le sur-corps soit scindés, c’est-à-dire se décomposent en produit de polynômes du premier degré. Si α est une racine de P(X) dans Ω alors K[α], corps engendré par K et α est un corps de rupture du polynôme. La proposition suivante établit le lien entre le corps de rupture et les sous-corps de la clôture algébrique isomorphes au corps de rupture.

Un polynôme est dit séparable s'il n'admet pas de racine multiple dans Ω (ce qui équivaut à dire qu'il est premier à son polynôme dérivé). C'est souvent le cas pour un polynôme irréductible, c'est toujours vrai sur un corps parfait (par exemple le corps des nombres rationnels, le corps des nombres réels ou tout corps de caractéristique nulle; c'est également le cas des corps finis). Voir l'article sur les extensions séparables pour plus de détails.