Corps de rupture - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques et plus précisément en algèbre dans le cadre de la théorie de Galois un corps de rupture d'un polynôme irréductible P(X) à coefficients dans un corps K est une extension algébrique minimale de K contenant au moins une racine du polynôme.
Selon les auteurs, on peut trouver d'autres définitions du corps de rupture (voir section ).
On démontre qu'avec la définition choisie, si P est un polynôme irréductible, tous les corps de rupture de P(X) sont isomorphes à K[X]/(P(X)), anneau K[X] des polynômes à coefficients dans K quotienté par l'idéal engendré par le polynôme P(X).
Un corps de rupture permet de trouver un corps dans lequel le polynôme peut être rompu mais, en général, cette construction ne suffit pas à scinder totalement le polynôme, c'est-à-dire à le décomposer en produit de facteurs du premier degré. La construction d'un corps de rupture n'est donc qu'un étape dans la construction des corps de décomposition dans lequel le polynôme pourra être totalement scindé. Ce sont les corps de décomposition qui, dans le cas où le critère de séparabilité est assuré, possèdent les bonnes propriétés nécessaires pour appliquer le théorème fondamental de la théorie de Galois.
Si un corps de rupture ne contient pas l'intégralité des racines de P(X), il est alors possible de réitérer l'opération jusqu'à ce qu'une extension algébrique contenant toutes les racines soit construite : on obtient le corps de décomposition du polynôme.
Définition
Soit K un corps et P(X) un polynôme formel irréductible à une indéterminée et à coefficients dans K. Si L est une extension de K dans laquelle P possède une racine α, alors le plus petit sous-corps de L contenant K et α, est l'extension simple de K définie par α et se note K(α). Un corps de rupture de P(X), polynôme irréductible sur K, est par définition une extension simple K(α) de K, où α est une racine de P. Alors α est algébrique sur K, et P (qui est irréductible) est, à un inversible près, le polynôme minimal de α sur K.
Une extension L d'un corps K peut être vue comme un espace vectoriel sur K, dont la dimension s'appelle le degré de L sur K et se note [L:K]. Un corps de rupture de P sur K est une extension algébrique finie de K. On montre dans le paragraphe suivant que, le polynôme P étant irréductible, le degré de cette extension est forcément le degré n du polynôme P, puisque, α étant une racine de P, K(α) est K[α], le plus petit anneau engendré par K et α, espace vectoriel de base 1, α, …, αn-1 sur K.
Par conséquent un corps de rupture F de P polynôme irréductible de degré n sur K est de façon équivalente :
- une extension (algébrique) simple de K définie par une racine de P ;
- une extension minimale de K contenant une racine de P, « minimale » signifiant qu'aucun sous-corps propre de F ne contient de racine de P(X) ;
- une extension de K contenant au moins une racine de P et de degré minimum sur K ;
- une extension de K contenant au moins une racine de P et de degré n sur K.
Exemples
- Dans le corps des nombres réels, le polynôme X2 + 1 ne possède, dans son corps de coefficients, aucune racine. En effet, tout carré du corps des nombres réels est positif. Un corps de rupture de ce polynôme est celui des nombres complexes. Il est de degré 2 sur
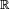
- Dans le corps des nombres rationnels, le polynôme X3 - 2 ne possède pas de racine dans
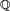
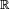
![\scriptstyle \sqrt[3] 2](https://static.techno-science.net/illustration/Definitions/autres/f/f1ef5a9b22cf71554f98e8bb07aac868_98b9611c6ebcff4d6b5f5c61f8a8a865.png)
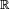
![\scriptstyle \Q(\sqrt[3]{2})](https://static.techno-science.net/illustration/Definitions/autres/b/b2637abdf9795da63864fd73c6d38dc7_309e117974b1da82cf0b1c78682fc943.png)
![\scriptstyle a+b\sqrt[3] 2+ c\sqrt[3]{4}](https://static.techno-science.net/illustration/Definitions/autres/c/c892b4fd0a6ee831ec51ab6ab8ebbcc1_5b6af50330dfbe70a0e8865e3ae6a631.png)
![\scriptstyle\sqrt[3]2 \mathrm j](https://static.techno-science.net/illustration/Definitions/autres/9/96f0b35b0f22b2ea10dadb09dd9d569e_8b6e819eaff4d3877d25e51211543df5.png)
![\scriptstyle\sqrt[3]2 \mathrm j^2](https://static.techno-science.net/illustration/Definitions/autres/9/9d0bdc2eca1b6a540047502c3173cccc_67759831d23e1edd30289007d21f3fb4.png)
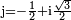
![\scriptstyle \Q(\sqrt[3]{2})](https://static.techno-science.net/illustration/Definitions/autres/b/b2637abdf9795da63864fd73c6d38dc7_309e117974b1da82cf0b1c78682fc943.png)
![\scriptstyle \Q(\sqrt[3]{2}\mathrm j)](https://static.techno-science.net/illustration/Definitions/autres/7/7a780c974f969cc2016ccd5e79e2e192_5200187d9b2ecd1f5d292ecf1d1157fd.png)
![\scriptstyle a+b\sqrt[3] 2j+ c\sqrt[3]{4}j^2](https://static.techno-science.net/illustration/Definitions/autres/1/11557d61c5f5df7aa40b669a5dc4e622_2531b68ccdce5e8ebbe486361b2a8855.png)
![\scriptstyle \Q(\sqrt[3]{2}\mathrm{j}^2)](https://static.techno-science.net/illustration/Definitions/autres/6/6e940a2d0812beabe62e84600bdf0db5_aa1b6344a0590eb409c2992cc3a1b0e7.png)
- Un corps de rupture d'un polynôme irréductible peut être égal au corps de décomposition de celui-ci, même si le degré du polynôme est strictement supérieur à 2. C'est le cas pour le corps de rupture sur