Critère de divisibilité - Définition

Introduction

En mathématiques et plus précisément en arithmétique modulaire, un critère de divisibilité est une particularité d'un entier permettant de déterminer si ce nombre est divisible par un autre. Malgré leur apparence de « recette de cuisine » (voir la liste de critères de divisibilité), les critères de divisibilité sont basés sur des démonstrations mathématiques ; il est possible d'en trouver pour n'importe quel nombre grâce aux congruences.

Recherche d'un critère de divisibilité

Pour chercher un critère de divisibilité du nombre p en base 10, il suffit de chercher un multiple de p ayant une différence de 1 avec un multiple de 10, noté 10k.

Il suffit alors de multiplier le chiffre des unités par cet entier k et de l'ôter du nombre de dizaines. Par exemple pour 7485 et la divisibilité par 7, on retranche 2 × 5 à 748 et on recommence avec le résultat ainsi formé. Le nombre initial sera un multiple de p si et seulement si le nombre final est un multiple de p (voir démonstration plus bas)

Exemples :

• 3 × 3 = 9 = 1 × 10 – 1 donc il faudra ajouter les chiffres pour la divisibilité par 3 et par 9
• 3 × 7 = 2 × 10 + 1 donc il faudra retrancher les doubles des chiffres pour la divisibilité par 7 (et par 3)
• 11 = 1 × 10 + 1 donc il faudra retrancher les chiffres pour la divisibilité par 11
• 13 × 3 = 4 × 10 – 1 donc il faudra ajouter les quadruples des chiffres pour la divisibilité par 13 (et par 3)
• 17 × 3 = 5 × 10 + 1 donc il faudra retrancher les quintuples des chiffres pour la divisibilité par 17 (et par 3)
• 29 = 3 × 10 – 1 donc il faudra ajouter les triples des chiffres pour la divisibilité par 29
• 31 = 3 × 10 + 1 donc il faudra retrancher les triples des chiffres pour la divisibilité par 31
• 41 = 4 × 10 + 1 donc il faudra retrancher les quadruples des chiffres pour la divisibilité par 41
• etc.

Démonstration pour un nombre quelconque

De manière générale, pour déterminer si un nombre A est divisible par d, on procède en plusieurs étapes

• on décompose d sous la forme où d' est premier avec 10
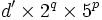
• d divise A si et seulement si d' , 2^q et 5^p divisent A.

Divisibilité par 2^q

A est divisible par 2^q si et seulement si le nombre formé par les q premiers chiffres (en partant de l'unité) est divisible par 2^q

Exemple:

79 532 512 est divisible par 16 (= 2⁴) car 2512 est divisible par 16

Démonstration

10^q est multiple de 2^q , donc on peut se débarrasser de toute la partie du nombre multiple de 10^q

Divisibilité par 5^p

A est divisible par 5^p si et seulement si le nombre formé par les p premiers chiffres (en partant de l'unité) est divisible par 5^p

Exemple:

9864375 est divisible par 125 (= 5³) car 375 est divisible par 125

Démonstration

10^p est multiple de 5^p , donc on peut se débarrasser de toute la partie du nombre multiple de 10^p

Divisibilité par d' premier avec 10

Puisque d' est premier avec 10, il existe un entier k tel que . C'est l'application du théorème de Bachet-Bézout. Alors le nombre A sera divisible par d' si et seulement si le nombre est multiple de d'

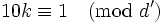
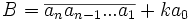
Démonstration

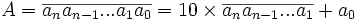
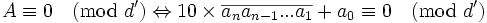
Comme k est premier avec d', on peut multiplier la congruence par k en conservant l'équivalence, et comme , on a

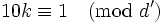
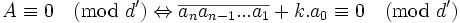
Exemple

La première difficulté est de trouver cet entier k (le plus proche de 0 possible). Par exemple , pour d' = 7, cet entier est -2 car , et pour d' = 93, cet entier est 28 car

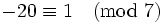
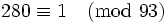
Ensuite, il suffit de réitérer autant que fois que nécessaire le principe précédent : pour vérifier, par exemple, que 111258 est divisible par 7

111258 est divisible par 7 si et seulement si 11125 - 2 × 8 , c’est-à-dire 11109, est divisible par 7

11109 est divisble par 7 si et seulement si 1110 - 18, c’est-à-dire 1092 l'est aussi

1092 est divisible par 7 si et seulement si 109 - 4, c’est-à-dire 105 est divisible par 7

enfin 105 est divisible par 7 car 10 - 2× 5, c’est-à-dire 0 est divisible par 7

Cette méthode a l'avantage de se terminer au bout de n étapes si le nombre est de l'ordre de 10ⁿ. On peut raccourcir ce travail pour les très grands nombres en cherchant le plus petit entier m tel que . Cet entier existe dès que d' est premier. On découpe alors le nombre A par tranches de m chiffres, on ajoute entre eux les nombres issus de ce découpage, on obtient ainsi un nombre B dont l'ordre de grandeur est voisin de 10^m. A sera divisible par d' si et seulement si B l'est.

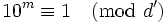
Exemple: donc pour la divibilité par 7, on découpera en tranches de 6.

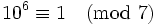
109 826304 est divisible par 7 si et seulement si 826304 + 109, c’est-à-dire 826413 l'est , si et seulement si 82641 - 6 (= 82635) l'est, si et seulement si 8263-10 (=8253) l'est, si et seulement si 825-6 (= 819) l'est, si et seulement si 81-18 (= 63) l'est.