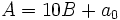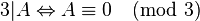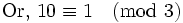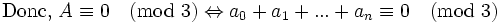Critère de divisibilité - Définition

Exemple et démonstration de critères de divisibilité

Avant d'aborder la méthode générale, sont présentées ici quelques critères de divisibilité qui illustrent les techniques utilisées. Une liste très complète des critères de divisibilité figurent dans l'article liste de critères de divisibilité .

On aborde les démonstrations dans car un entier relatif a les mêmes diviseurs que sa valeur absolue.

Ci-dessous sont expliquées les notations utilisées dans le reste de l'article.

Soit A un entier naturel.

On pose , c'est-à-dire que a₀ est le chiffre des unités, a₁ est le chiffre des dizaines, etc.

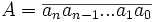
d'où

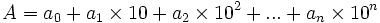
Le symbole utilisé dans l'article est l'opérateur de l'addition, il se nomme sigma.

par 2

Énoncé

Un nombre est divisible par 2 si son chiffre des unités est 0;2;4;6;8.

Démonstration

10B est toujours multiple de 2 donc A est multiple de 2 si et seulement si a₀ est multiple de 2.

par 3

Énoncé

Un nombre est divisible par 3 si la somme de ses chiffres est divisible par 3.

Démonstration

Soit A un entier naturel divisible par 3.

Conclusion : Lorsqu'un nombre est divisible par 3, la somme des chiffres de ce nombre est divisible par 3.

Remarque, par une démonstration analogue, on démontre aussi qu'un nombre est divisible par 9 si la somme de ses chiffres est divisible par 9. (puisque )

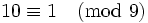
par 7

Énoncé 1

Un nombre est divisible par 7 si et seulement si le résultat de la soustraction du nombre de dizaines (à ne pas confondre avec chiffre des dizaines) par le double du chiffre des unités est divisible par 7.

Exemple : 252

nombre des dizaines: 25; chiffre des unités: 2

On a, 2x2=4 Donc 25-4=21

Démonstration

Soit A un entier naturel divisible par 7,

On a :

Or, 7 et 10 sont premiers entre eux, donc d'après le théorème de Gauss :

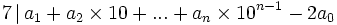
Réciproquement, si

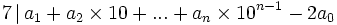
alors

Or, donc

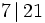
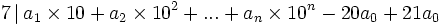
On obtient :

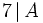
Conclusion :

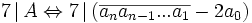
Enoncé 2

En utilisant la clé de divisibilité : 1, 3, 2, 6, 4, 5. Celle-ci s'obtient avec les reste de la division de 1 par 7. Elle est aussi valable pour tout les autres diviseurs.

On multiplie par le chiffre correspondant de la clé chaque chiffre du nombre à analyser en commencant par les unités.

Exemple

est-ce que 19231 est divisible par 7 ?

1 x 1 = 1, 3 x 3 = 9, 2 x 2 = 4, 6 x 9 = 54, 4 x 1 = 4

1 + 9 + 4 + 54 + 4 = 72

72 n'est pas un multiple de 7 donc 19231 n'est pas divisible par 7.

est-ce que 21357 est divisible par 7 ?

1 x 7 = 7, 3 x 5 = 15, 2 x 3 = 6, 6 x 1 = 6, 4 x 2 = 8

7 + 15 + 6 + 6 + 8 = 42

42 est un multiple de 7 donc 21357 est divisible par 7.

Bibliographie

• D, André. La jubilation en mathématiques. Paris : ACL — Les éditions du Kangourou, 2005. 32 pages.

Remarque sur la complexité algorithmique

In fine, on peut trouver de cette manière pour chaque nombre d un critère de divisibilité par d. Il faut d'abord remarquer qu'un critère général, manipulable algorithmiquement, préexiste : pour savoir si un nombre A est divisible par d, il suffit de calculer la division euclidienne de A par d, et de tester l'annulation du reste. Un tel calcul s'effectue en un nombre d'opérations contrôlé par le nombre de chiffres de A (complexité linéaire).

Les algorithmes présentés ici sont en fait précisément des variantes de cet algorithme général : on a vu en effet qu'on les obtient via un calcul modulaire, qui repose sur la notion de division euclidienne. Leur complexité est à nouveau linéaire : en effet, à chaque étape de calcul, on est ramené à tester la division par d d'un nombre ayant un chiffre de moins que le nombre précédent, et le nombre d'étapes total sera encore de l'ordre du nombre de chiffre du nombre A initial. Pour un calcul à la main en base 10, du moins pour les petites diviseurs d, ces méthodes ont un avantage, par rapport à la méthode générale par division euclidienne : on évite les calculs intermédiaires de division.

Il faut toutefois noter que ces méthodes ne fournissent qu'un critère de divisibilité, alors que la méthode générale est plus précise et fournit quotient et reste.