Crochet de Poisson - Définition

Introduction

En mécanique hamiltonienne, on définit le crochet de Poisson de deux observables A et B, c'est-à-dire de deux fonctions sur l'espace des phases, par :

où les 2N variables canoniques sont :

• les N coordonnées généralisées {qⁱ}_{i = 1,...,N}.
• les N moments conjugués {p_i}_{i = 1,...,N}.

Propriétés

• Le crochet de Poisson est antisymétrique :
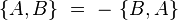
• Le crochet de Poisson apporte une structure d'algèbre à l'ensemble des observables, qui en mécanique classique sont des fonctions sur l'espace des phases :

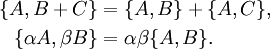
• Le crochet de Poisson satisfait à l'identité de Jacobi :

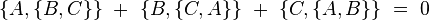
• Les variables canoniques sont liées par les relations :
• car les dérivées partielles commutent.

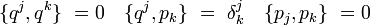
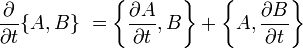
Évolution d'une observable quelconque

Cas général

Soit une observable A, c’est-à-dire une fonction sur l'espace des phases dépendant des moments et des coordonnées généralisées. Il résulte des relations précédentes que :

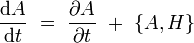
où désigne la dérivée partielle de A par rapport à une éventuelle dépendance explicite de A par rapport au temps.

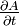
Cas de l'énergie totale

On obtient pour l'énergie totale du système :

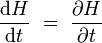
puisque {H,H} = 0 par antisymétrie.

Théorème de Poisson

Si A et B sont deux « intégrales premières » du système, c'est-à-dire si , alors en est une aussi.

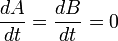
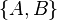
Démonstration :

Dans le cas où A et B ne dépendent pas explicitement du temps : d'après l'identité de Jacobi, on a .

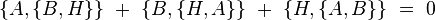
Or et , donc .

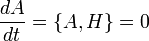
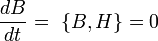
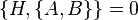
Comme ne dépend pas non plus explicitement du temps, on a .

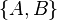
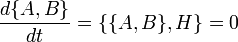
D'où la conclusion pour ce cas.

Dans le cas général : on a

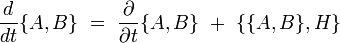
En utilisant l'identité de Jacobi et l'égalité utilisant les dérivées partielles, on obtient

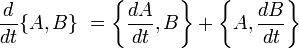
La conclusion dans le cas général est alors évidente.

Équations canoniques

Soit H(qⁱ,p_i) le hamiltonien du système considéré. Les équations canoniques de Hamilton se réécrivent à l'aide du crochet de Poisson sous la forme :

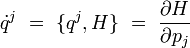
et :

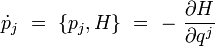
ou encore, de manière unifiée :

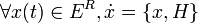
où E est l'espace des phases associé à la formulation hamiltonienne.

Quantification canonique

L'intérêt du crochet de Poisson est qu'il permet de passer facilement à la quantification dans le formalisme algébrique de Heisenberg de la mécanique quantique. Il suffit en général de faire une substitution :

où [.,.] désigne le commutateur, pour obtenir les relations de commutation des opérateurs dans le formalisme de Heisenberg à partir des crochets de Poisson des observables classiques. La même stratégie est applicable à la quantification d'un champ classique.