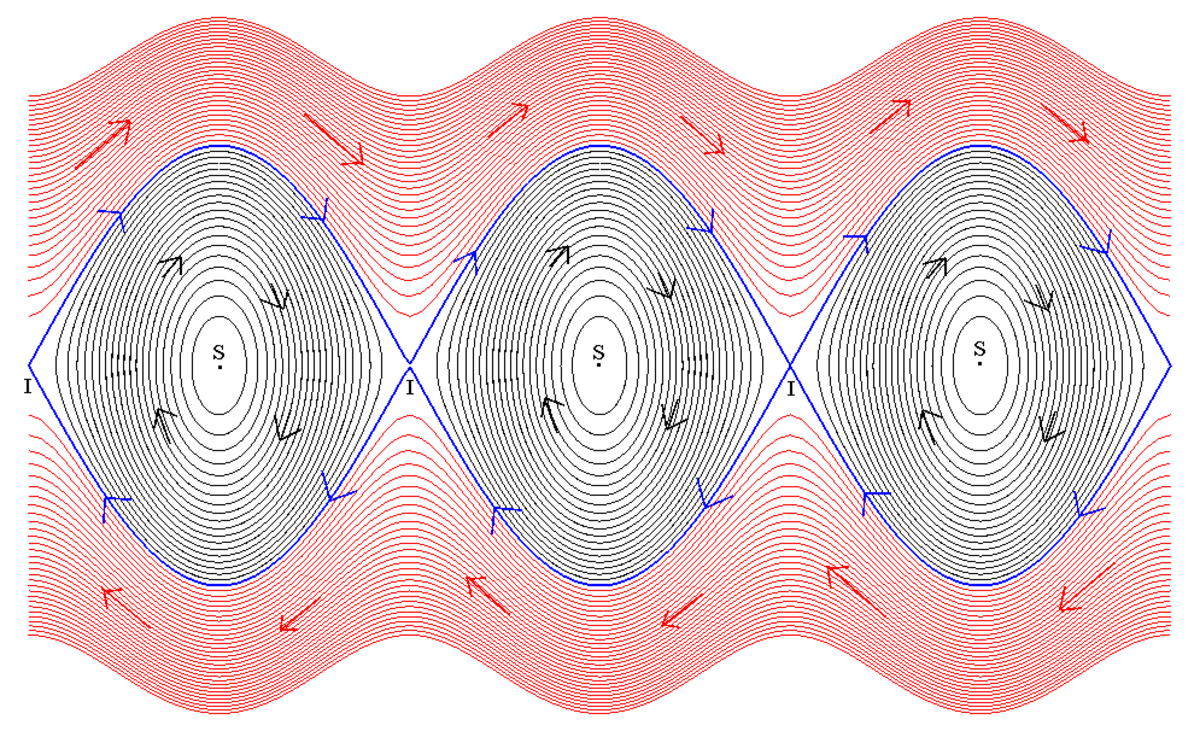
Courbes intégrales pour l'équation du pendule simple dans l'espace des phases (y,y')

L'espace des phases est un espace abstrait dont les coordonnées sont les variables dynamiques du système étudié.

Utilité d'un espace des phases (L'espace des phases est un espace abstrait dont les coordonnées sont les variables dynamiques du système étudié.)

Un exemple très schématique permet de fixer les idées.

Prenons par exemple un jeu vidéo (La vidéo regroupe l'ensemble des techniques, technologie, permettant l'enregistrement ainsi que la restitution d'images animées, accompagnées ou non de son, sur un support adapté à l'électronique et non de type photochimique. Le mot vidéo...) simulant la pose sur la Lune (La Lune est l'unique satellite naturel de la Terre et le cinquième plus grand satellite du système solaire avec un diamètre de 3 474...) d'un module d'exploration (L'exploration est le fait de chercher avec l'intention de découvrir quelque chose d'inconnu.) lunaire (Pour les homonymes, voir Pierrot lunaire, une œuvre de musique vocale d'Arnold Schönberg.) (Lunar Exploration Module, LEM) : le joueur peut activer la propulsion (La propulsion est le principe qui permet à un corps de se mouvoir dans son espace environnant. Elle fait appel à un propulseur qui transforme en force motrice l'énergie fournie par le milieu...) pour ralentir la chute, et doit donc doser entre la gravité (La gravitation est une des quatre interactions fondamentales de la physique.), qui fait descendre le module, et la propulsion (si celle-ci est trop forte, le module remonte). Si l'on ne voit sur son écran (Un moniteur est un périphérique de sortie usuel d'un ordinateur. C'est l'écran où s'affichent les informations saisies ou demandées par l'utilisateur et générées ou...) que la hauteur (La hauteur a plusieurs significations suivant le domaine abordé.) de l'engin par rapport au sol et que l'on estime au jugé sa vitesse (On distingue :) verticale (La verticale est une droite parallèle à la direction de la pesanteur, donnée notamment par le fil à plomb.), cette opération est longue et difficile.

Si en revanche on lui associe un petit diagramme (Un diagramme est une représentation visuelle simplifiée et structurée des concepts, des idées, des constructions, des relations, des données statistiques, de l'anatomie etc. employé dans tous les aspects des activités humaines...) matérialisant la situation (En géographie, la situation est un concept spatial permettant la localisation relative d'un espace par rapport à son environnement proche ou non. Il...) par un simple point (Graphie) dans un système de coordonnées à deux dimensions (Dans le sens commun, la notion de dimension renvoie à la taille ; les dimensions d'une pièce sont sa longueur, sa largeur et sa profondeur/son épaisseur, ou bien son diamètre si c'est une pièce de...) (altitude, vitesse), le pilotage en est considérablement facilité : l'objectif est matérialisé par un point fixe (En mathématiques, pour une application f d’un ensemble E dans lui-même, un élément x de E est un point fixe de f si f(x) = x.) à atteindre : le point (0,0) " au niveau du sol et sans vitesse ", ce qui constitue bien la définition (Une définition est un discours qui dit ce qu'est une chose ou ce que signifie un nom. D'où la division entre les définitions réelles et les définitions nominales.) de l'aterrissage. Le problème en devient si simple qu'il peut être automatisé.

Or la vitesse n'est que la dérivée (La dérivée d'une fonction est le moyen de déterminer combien cette fonction varie quand la quantité dont elle dépend, son argument, change. Plus précisément, une dérivée est une expression (numérique ou...) de l'autre coordonnée, la position : c'est un exemple de construction et d'utilisation d'un espace des phases très simple, et d'en tirer immédiatement profit.

Justifications de l'utilisation d'un espace des phases

Les coordonnées utilisées dans cet espace sont celle des variables canoniques de la mécanique (Dans le langage courant, la mécanique est le domaine des machines, moteurs, véhicules, organes (engrenages, poulies, courroies, vilebrequins, arbres de...) hamiltonienne. L'étude de la mécanique dans cet espace permet d'éliminer la contrainte temporelle dans l'étude de l'évolution d'un système. Cela se montre particulièrement utile quand on compare par exemple la dépendance des solutions d'une équation (En mathématiques, une équation est une égalité qui lie différentes quantités, généralement pour poser le problème de leur identité. Résoudre...) différentielle à ses conditions initiales.

Espace des phases pour un mobile ponctuel (En géométrie, un point est le plus petit élément constitutif de l'espace de travail.)

Les variables dynamiques sont au nombre (La notion de nombre en linguistique est traitée à l’article « Nombre grammatical ».) de 6 : 3 variables de position (x, y, z) et trois variables de quantité de mouvement (En physique, la quantité de mouvement est la grandeur physique associée à la vitesse et la masse d'un objet. La quantité de mouvement d'un système fait partie, avec l'énergie, des valeurs qui se conservent lors des...) (P_x, P_y, P_z).

D'après les équations de la mécanique, l'évolution d'un système est entièrement déterminée par la donnée (Dans les technologies de l'information, une donnée est une description élémentaire, souvent codée, d'une chose, d'une transaction, d'un événement, etc.) initiale de la position (x, y, z) et de la vitesse (v_x, v_y, v_z) — la masse (Le terme masse est utilisé pour désigner deux grandeurs attachées à un corps : l'une quantifie l'inertie du corps (la masse inerte) et...) étant connue, la quantité (La quantité est un terme générique de la métrologie (compte, montant) ; un scalaire, vecteur, nombre d’objets ou d’une autre manière de dénommer la valeur d’une collection ou un groupe de choses.) de mouvement est proportionnelle à vitesse.

Voir l'article Principe fondamental de la dynamique.

Cas de l'espace du vecteur (En mathématiques, un vecteur est un élément d'un espace vectoriel, ce qui permet d'effectuer des opérations d'addition et de multiplication par un scalaire. Un n-uplet...) d'onde (Une onde est la propagation d'une perturbation produisant sur son passage une variation réversible des propriétés physiques locales. Elle transporte de...)

Une onde peut se caractériser par son vecteur d'onde noté , qui est le vecteur :

• perpendiculaire (En géométrie plane, on dit que deux droites sont perpendiculaires quand elles se coupent en formant un angle droit. Le terme de perpendiculaire vient du latin...) au front d'onde ;
• orienté dans le sens (SENS (Strategies for Engineered Negligible Senescence) est un projet scientifique qui a pour but l'extension radicale de l'espérance de vie humaine. Par une évolution...) de propagation de l'onde ;
• dont la norme (Une norme, du latin norma (« équerre, règle ») désigne un état habituellement répandu ou moyen considéré le...) est l'inverse (En mathématiques, l'inverse d'un élément x d'un ensemble muni d'une loi de composition interne · notée multiplicativement, est un élément y tel que x·y =...) de la longueur (La longueur d’un objet est la distance entre ses deux extrémités les plus éloignées. Lorsque l’objet est filiforme ou en...) d'onde (voir aussi l'article Nombre d'onde).

Certaines personnes préfèrent définir la norme du vecteur d'onde comme étant l'inverse de la longueur d'onde multiplié par deux fois le nombre pi (ceci change la forme des équations, le terme 2π apparaissant ou pas dans l'équation de l'onde).

Voir l'article Espace réciproque.