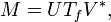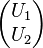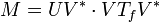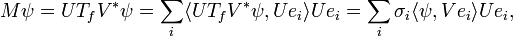Décomposition en valeurs singulières - Définition

Opérateurs bornés sur les espaces de Hilbert

La factorisation M = UΣV ^* peut être étendue comme opérateur borné M sur un espace de Hilbert H. D'une façon générale, pour tout opérateur borné M, il existe une isométrie partielle U, un vecteur unitaire V, un espace de mesure (X, μ) et f mesurable positive telle que :

où T_f est la mutliplication par f sur L²(X, μ).

On peut le montrer en travaillant l'argument d'algèbre linéaire utilisé pour le cas matriciel. VT_f V* est l'unique racine positive de M*M, donnée par l'analyse fonctionnelle de Borel, pour les opérateurs auto-adjoints. La raison pour laquelle U n'a pas besoin d'être unitaire est liée au fait que, contrairement au cas de dimension finie, étant donnée une isométrie U₁ avec un noyau non trivial, une isométrie U₂ existe telle que :

est un opérateur unitaire.

Puisque, pour les matrices, la décomposition en valeurs singulières est équivalente à la décomposition polaire pour les opérateurs, on peut réécrire cela sous la forme :

et remarquer que U V* est encore une isométrie partielle tant que VT_f V* est positif.

Valeurs singulières et opérateurs compacts

Pour étendre la notion de valeur singulière et de vecteurs singuliers au cas des opérateurs, on doit se restreindre aux opérateurs compacts sur les espaces de Hilbert. On rappelle certaines propriétés utiles :

• Les opérateurs compacts sur les espaces de Banach, donc de Hilbert, possèdent un spectre discret ;
• Si T est compact, tout λ de son spectre, non-nul, est une valeur propre ;
• Un opérateur compact auto-adjoint peut être diagonalisé par ses vecteurs propres ;
• Si M est compact, alors M*M l'est également.

En utilisant la diagonalisation, l'image unitaire de la racine carrée positive de M, notée T_f, possède une famille orthonormale de vecteurs propres {e_i}, correspondants aux valeurs propres strictement positives {σ_i}. Pour tout ψ ∈ H,

quand la série converge normalement dans H. On remarque que cette expression est proche de celle dans le cas de dimension finie.

Les σ_i sont appelées valeurs singulières de M. {U e_i} et {V e_i} sont analogues aux vecteurs singuliers à gauche et à droite respectivement pour M.

Calcul de la SVD

Le calcul explicite, analytique, de la décomposition en valeurs singulières d'une matrice est difficile dans le cas général. On utilise, en particulier dans les applications, des algorithmes spécialisés.

La procédure DGESVD de la librairie LAPACK propose une approche courante pour le calcul de la décomposition en valeurs singulières d'une matrice. Si la matrice possède plus de lignes que de colonnes, on effectue tout d'abord une décomposition QR. Le facteur R est ensuite réduit sous forme bidiagonale. Pour ceci, on peut effectuer des transformations de Householder alternativement sur les colonnes et sur les lignes de la matrice. Les valeurs singulières et vecteurs singuliers sont alors trouvés en effectuant une itération de type QR bidiagonale avec la procédure DBDSQR.

GNU Scientific Library propose trois alternatives : l'algorithme de Golub-Reinsch, l'algorithme de Golub-Reinsch modifié (plus rapide pour les matrices possédant bien plus de lignes que de colonnes) et l'orthogonalisation de Jacobi.