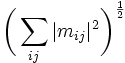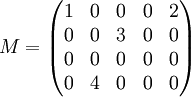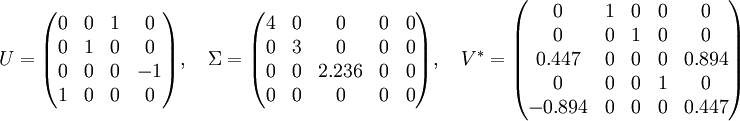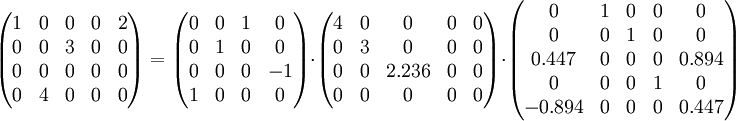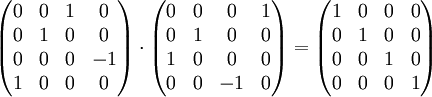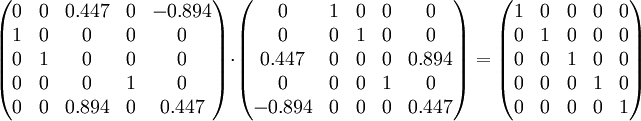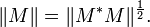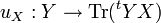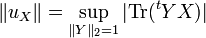Décomposition en valeurs singulières - Définition

Exemple

Soit la matrice :

La décomposition en valeurs singulières de M est alors :

Ainsi, on a :

On vérifie que Σ ne possède des valeurs non nulles que sur sa diagonale. De plus, comme montré ci-dessous, en multipliant les matrices U et V ^* par leurs transposées, on obtient la matrice identité :

Et de même :

Histoire

La décomposition en valeurs singulières fut développée à l'origine par les mathématiciens étudiant la géométrie différentielle, qui désiraient déterminer si une forme bilinéaire réelle pouvait en égaler une autre par des transformations orthogonales indépendantes des deux espaces concernés.

Eugenio Beltrami et Camille Jordan ont découvert indépendamment, en 1873 et 1874 respectivement , que les valeurs singulières des formes bilinéaires, représentées sous forme matricielle, constituaient un ensemble complet d'invariants pour les formes bilinéaires subissant des substitutions orthogonales.

James Joseph Sylvester s'intéressa également à la décomposition en valeurs singulières en 1889 pour les matrices réelles carrées, apparemment indépendamment des travaux de Beltrami et Jordan. Sylvester donna aux valeurs singulières le nom de « multiplicateurs canoniques » d'une matrice A.

Le quatrième mathématicien à l'origine de la découverte de cette décomposition est Autonne, en 1915. Il aboutit à ce résultat au travers de la décomposition polaire.

La première preuve de la décomposition en valeurs singulières pour les matrices rectangulaires et complexes est attribuée à Eckart et à Young, en 1936.

En 1907, Erhard Schmidt définit l'analogue des valeurs singulières pour les opérateurs intégraux (qui, à certaines conditions près, sont compacts) ; il semble qu'il ne connaissait pas les travaux parallèles sur les valeurs singulières des matrices de dimension finie. Cette théorie fut développée encore par le mathématicien français Émile Picard en 1910, qui est à l'origine du terme moderne de « valeurs singulières » qu'il notait σ_k.

Avant 1965, aucune méthode efficace de calcul de cette décomposition n'était connue. Gene Golub et William Kahan proposèrent un premier algorithme cette année, puis, en 1970, Golub et Christian Reinsch publièrent une variante de l'algorithme Golub/Kahan qui demeure aujourd'hui le plus utilisé.

La généralisation de cette décomposition à deux, trois ou N dimensions est encore un sujet de recherche active, puisqu'elle se révèle d'un intérêt majeur dans de nombreux domaines.

Normes

Normes de Ky Fan

La somme des k plus grandes valeurs singulières de M est une norme sur l'espace vectoriel des matrices, appelée norme de Ky Fan ou norme k de M.

La première des normes de Ky Fan, la norme 1 de Ky Fan, est la même que la norme d'opérateur de M en tant qu'opérateur linéaire, selon les normes euclidiennes de K^m et Kⁿ. En d'autres termes, la norme 1 de Ky Fan est la norme d'opérateur induite par le produit intérieur euclidien standard l². Pour cette raison, on l'appelle également norme 2 d'opérateur. On peut facilement vérifier la relation en la norme 1 de Ky Fan et les valeurs singulières. C'est vrai en général, pour un opérateur borné M sur un espace de Hilbert (potentiellement infini) :

Cependant, dans le cas des matrices, M*M^½ est une matrice normale, donc ||M*M||^½ est la plus grande valeur propre de M*M^½, donc la plus grande valeur singulière de M.

La dernière norme de Ky Fan, qui est égale à la somme de toutes les valeurs singulières, est la norme de trace définie par ||M|| = Tr (M*M)^½.

On considère la forme linéaire définie dans l'algèbre des matrices d'ordre n par:

On considère la norme spectrale des matrices et l'on définit la norme duale de u_X par:

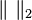
On vérifie alors aisément que cette norme duale est en fait la norme trace de X définie ci-dessus. De plus, cette norme est une norme d'algèbre.

Norme de Hilbert-Schmidt

Les valeurs singulières sont liées à une autre norme sur l'espace des opérateurs. On considère le produit intérieur de Hilbert-Schmidt sur les matrices n × n, défini par <M, N> = Tr N*M. Alors la norme induite est ||M|| = <M, M>^½ = (Tr M*M)^½. La trace étant un invariant d'équivalence unitaire, cela implique que :

,

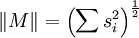
où les s_i sont les valeurs singulières de M. On l'appelle norme de Frobenius, norme 2 de Schatten ou norme de Hilbert-Schmidt de M. On montre également que si :

,

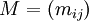
alors cette norme coïncide avec :

.